【题目】如图,有一个不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是
参考答案:
【答案】![]()
( ![]() )
)
【解析】解:因为AC为对角线,故当AC最小时,正方形边长此时最小.
①当 A、C都在对边中点时(如下图所示位置时),显然AC取得最小值,
∵正六边形的边长为1,
∴AC=![]() ,
,
∴a2+a2=AC2=![]() .
.
∴a=![]() =
=![]() .
.
②当正方形四个顶点都在正六边形的边上时,a最大(如下图所示).
设A′(t,![]() )时,正方形边长最大.
)时,正方形边长最大.
∵OB′⊥OA′.
∴B′(-![]() , t)
, t)
设直线MN解析式为:y=kx+b,M(-1,0),N(-![]() , -
, -![]() )(如下图)
)(如下图)
∴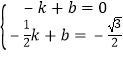 .
.
∴![]() .
.
∴直线MN的解析式为:y=![]() (x+1),
(x+1),
将B′(-![]() , t)代入得:t=
, t)代入得:t=![]() -
-![]() .
.
此时正方形边长为A′B′取最大.
∴a=![]() =3-
=3-![]() .
.
故答案为:![]() ≤a≤3-
≤a≤3-![]() .
.
分情况讨论.① 当A、C都在对边中点时,a最小.②当正方形四个顶点都在正六边形的边上时,a最大.根据题意求出正方形对角线的长度,再根据勾股定理即可求出a.从而得出a的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )

A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的
 时,则
时,则  为( )
为( )
A.
B.2
C.
D.4 -
科目: 来源: 题型:
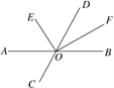
查看答案和解析>>【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
-
科目: 来源: 题型:
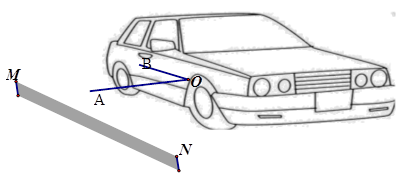
查看答案和解析>>【题目】如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
-
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
(1)如图2,在直角坐标系中,直线l1:y=
 x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.

相关试题

