搜索
【题目】如图，在平面直角坐标系中，矩形OABC的对角线OB、AC相交于点D，BE∥AC，AE∥OB．函数
（k＞0，x＞0）的图象经过点E．若点A、C的坐标分别为（3，0）、（0，2），则k的值为（ ）
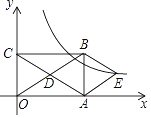
A. 3 B. 4 C. 4.5 D. 6
参考答案：
【答案】C
【解析】解：∵BE∥AC，AE∥OB，
∴四边形AEBD是平行四边形，
∵四边形OABC是矩形，C的坐标为（0，2），
∴DA=
AC，DB=
OB，AC=OB，AB=OC=2，
∴DA=DB，
∴四边形AEBD是菱形；
连接DE，交AB于F，如图所示：
∵四边形AEBD是菱形，
∴AB与DE互相垂直平分，
∵OA=3，OC=2，
∴EF=DF=
OA=
，AF=
AB=1，3+
=
，
∴点E坐标为：（
，1）．
∵函数
（k＞0，x＞0）的图象经过点E，
∴k=
×1= 
．
故答案为：C．
-
科目： 来源： 题型：
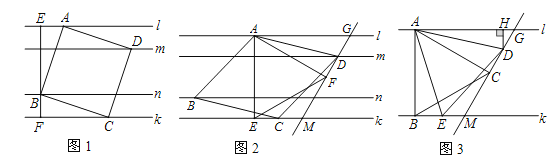
查看答案和解析>>【题目】【背景】已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1，d2，d3，且d1＝d3＝1，d2＝2.我们把四个顶点分别在l，m，n，k这四条平行线上的四边形称为“格线四边形” ．
【探究1】(1)如图1，正方形ABCD为“格线四边形”，BE⊥l于点E，BE的反向延长线交直线k于点F.求正方形ABCD的边长．
【探究2】(2)如图2，菱形ABCD为“格线四边形”且∠ADC＝60°，△AEF是等边三角形，AE⊥k于点E，∠AFD＝90°，直线DF分别交直线l，k于点G、点M.求证：EC＝DF．
【拓展】(3)如图3，l∥k，等边△ABC的顶点A，B分别落在直线l，k上，AB⊥k于点B，且∠ACD＝90°，直线CD分别交直线l、k于点G、点M，点D、点E分别是线段GM、BM上的动点，且始终保持AD＝AE，DH⊥l于点H.猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，下列条件之一能使平行四边形ABCD是菱形的为_____________．
①AC⊥BD；②∠BAD=90°；③AB=BC；④AC=BD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线l所对应的函数表达式为y=x．过点A1（0，1）作y轴的垂线交直线l于点B1 ， 过点B1作直线l的垂线交y轴于点A2；过点A2作y轴的垂线交直线l于点B2 ， 则点B2的坐标为（ ）
A. （1，1） B. （
， 
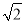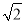） C. （2，2） D. （ 2
，2
） -
科目： 来源： 题型：
查看答案和解析>>【题目】某校对初三学生进行物理、化学实验操作能力测试．物理、化学各有3个不同的操作实验题目，物理实验分别用①、②、③表示，化学实验分别用a、b、c表示．测试时每名学生每科只操作一个实验，实验的题目由学生抽签确定，第一次抽签确定物理实验题目，第二次抽签确定化学实验题目．王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好．请用画树状图（或列表）的方法，求王刚同学同时抽到两科都准备得较好的实验题目的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义新运算“※”：a※b=2a+b则下列结论：①（-2）※5=1；②若x※（x-6）=0，则
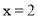；③存在有理数y，使y※（y+1）=y※（y-1）成立；④若m※n=5，m※（-n）=3，则
，
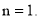其中正确的是 _______________(把所有正确结论的序号都选上). -
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，∠A＝30°，AD＝
，BD＝4，则平行四边形ABCD的面积等于 ______________.
相关试题
