【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
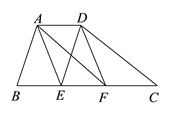
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
参考答案:
【答案】(1)AD=![]() BC;(2)见解析.
BC;(2)见解析.
【解析】分析:
(1)由AD∥BC,AB∥DE,AF∥DC,易得四边形ABED和四边形AFCD都是平行四边形,结合四边形AEFD是平行四边形可得AD=BE=EF=FC,由此可得AD=![]() BC;
BC;
(2)由(1)可知四边形ABED和四边形AFCD都是平行四边形,从而可得AB=DE,AF=DC结合AB=CD可得DE=AF,再结合四边形AEFD是平行四边形即可得到四边形AEFD是矩形的结论.
详解:
(1)∵AD∥BC,AB∥DE,AF∥DC,
∴四边形ABED和四边形AFCD都是平行四边形,
∴AD=BE,AD=CF,
∵四边形AEFD是平行四边形,
∴AD=EF,
∴AD=BE=EF=FC,
∴BC=BE+EF+FC=3AD,
∴AD=![]() BC;
BC;
(2)∵四边形ABED和四边形AFCD都是平行四边形,
∴DE=AB,AF=CD,
又∵AB=CD,
∴AF=DE,
又∵四边形AEFD是平行四边形,
∴平行四边形AEFD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

-
科目: 来源: 题型:
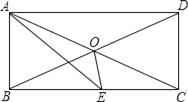
查看答案和解析>>【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线y=
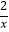 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= 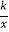 (k<0)上运动,则k的值是
(k<0)上运动,则k的值是 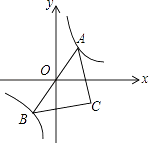
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线y=
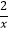 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=  (k<0)上运动,则k的值是
(k<0)上运动,则k的值是 
-
科目: 来源: 题型:
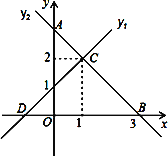
查看答案和解析>>【题目】如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有_____________.
①y1的解析式为y1=x+2②OA=OB③∠CDB=45°④△AOB≌△BCD.
相关试题

