【题目】已知二次函数y＝x2－4x＋3.

(1)用配方法求其图象的顶点C的坐标，并描述该函数的函数值随自变量的增减而变化的情况；

(2)求函数图象与x轴的交点A，B的坐标，及△ABC的面积．

参考答案：

【答案】（1）y＝ (x－2)2－1，（2）1

【解析】试题分析：（1）配方后求出顶点坐标即可；

（2）求出A、B的坐标，根据坐标求出AB、CD，根据三角形面积公式求出即可．

试题解析：（1）y=x2-4x+3

=x2-4x+4-4+3

=（x-2）2-1，

所以顶点C的坐标是（2，-1），

当x＜2时，y随x的增大而减少；

当x＞2时，y随x的增大而增大；

（2）解方程x2-4x+3=0

得：x1=3，x2=1，

即A点的坐标是（1，0），B点的坐标是（3，0），

过C作CD⊥AB于D，

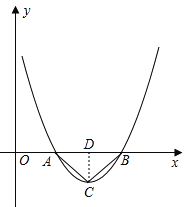
∵AB=2，CD=1，

∴S△ABC=AB×CD=×2×1=1．

关闭