【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.

参考答案:
【答案】(1)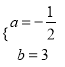 ;(2)S关于x的函数表达式为S=﹣x2+8x(2<x<6),面积S有最大值为16.
;(2)S关于x的函数表达式为S=﹣x2+8x(2<x<6),面积S有最大值为16.
【解析】试题分析:(1)把A与B坐标代入二次函数解析式求出a与b的值即可;
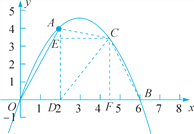
(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,分别表示出三角形OAD,三角形ACD,以及三角形BCD的面积,之和即为S,确定出S关于x的函数解析式,并求出x的范围,利用二次函数性质即可确定出S的最大值,以及此时x的值.
试题解析:
(1)将点A(2,4),B(6,0)的坐标分别代入y=ax2+bx,
得![]() 解得
解得
(2)如解图,过点A作x轴的垂线,垂足为D(2,0),过点C作CE⊥AD,CF⊥x轴,垂足分别为E,F,连结AC,BC,CD.
则S△OAD=![]() OD·AD=
OD·AD=![]() ×2×4=4,
×2×4=4,
S△ACD=![]() AD·CE=
AD·CE=![]() ×4×(x-2)=2x-4,
×4×(x-2)=2x-4,
S△BCD=![]() BD·CF=
BD·CF=![]() ×(6-2)×
×(6-2)×![]() =-x2+6x,
=-x2+6x,
∴S=S△OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x,
∴S关于x的函数表达式为S=-x2+8x(2<x<6).
∵S=-x2+8x=-(x-4)2+16,
∴当x=4时,四边形OACB的面积S有最大值,最大值为16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解方程:5+x=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】声音在空气中每小时约传播1200千米,将1200用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解方程:3x+6=31﹣2x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+9是完全平方式,则k的值是( )
A. 6 B. ﹣6 C. 9 D. 6或﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(x﹣2)(x+2)+x2(x﹣1),其中x=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,投掷这样的骰子一次,向上一面点数是偶数的结果有( )
A.1种
B.2种
C.3种
D.6种
相关试题

