【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
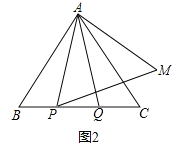
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

参考答案:
【答案】(1)40°;(2)①作图见解析;②证明见解析.
【解析】
试题分析:(1)根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,根据三角形外角的性质即可得到结论;
(2)①根据要求作出图形,如图2;
②根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.
试题解析:(1)∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ=20°,∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=60°﹣20°﹣20°=20°,∴∠BAQ=∠BAP+∠PAQ=40°;
(2)①如图2;
②∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ,∵点Q关于直线AC的对称点为M,∴AQ=AM,∠QAC=∠MAC,∴∠MAC=∠BAP,∴∠BAP+∠PAC=∠MAC+∠CAP=60°,∴∠PAM=60°,∵AP=AQ,∴AP=AM,∴△APM是等边三角形,∴AP=PM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用不等式表示“x与5的差不小于4”:.
-
科目: 来源: 题型:
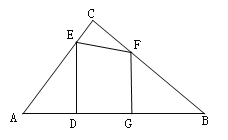
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设
 ,
,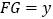 ,
,求
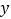 关于
关于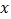 的函数解析式。
的函数解析式。(3)在点E、F移动过程中,△AED与△CEF能否相似,若能,求AD的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年,合肥市户籍人口数约为801.4万人,将801.4万用科学记数法表示应是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1、x2是一元二次方程x2+2x﹣3=0的二个根,则x1x2的值是( )
A.2
B.-2
C.3
D.-3 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算|﹣6﹣2|的结果是( )
A. ﹣8B. 8C. ﹣4D. 4
-
科目: 来源: 题型:
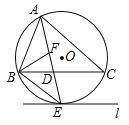
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
相关试题

