【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B. 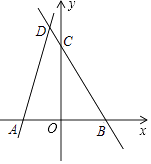
(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0). ①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
参考答案:
【答案】
(1)解:∵直线y=﹣2x+a与y轴交于点C (0,6),
∴a=6,
∴该直线解析式为y=﹣2x+6
(2)解:①∵点D(﹣1,n)在直线BC上,
∴n=﹣2×(﹣1)+6=8,
∴点D(﹣1,8).)
设直线AD的解析式为y=kx+b,
将点A(﹣3,0)、D(﹣1,8)代入y=kx+b中,
得: ![]() ,
,
解得: ![]() ,
,
∴直线AD的解析式为y=4x+12.
②令y=﹣2x+6中y=0,则﹣2x+6=0,解得:x=3,
∴点B(3,0).
∵A(﹣3,0)、D(﹣1,8),
∴AB=6.
S△ABD= ![]() AByD=
AByD= ![]() ×6×8=24.
×6×8=24.
③∵点M在直线y=﹣2x+6上,
∴M(m,﹣2m+6),
则 ![]()
当m<3时,S= ![]()
即S=﹣6m+18;
当m>3时, ![]()
即S=6m﹣18.
【解析】(1)将点C(0,6)代入y=﹣2x+a求得a的值即可;(2)①将点D坐标代入直线BD解析式可得n的值,再利用待定系数法可求得直线AD解析式;②根据三角形面积公式即可得;③设M(m,﹣2m+6),根据面积公式可得函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段a,b,c,d成比例线段,其中a=3cm,b=4cm,c=6cm,则d=_____cm;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( ).
A.所有等腰三角形都相似B.两边成比例的两个等腰三角形相似
C.有一个角相等的两个等腰三角形相似D.有一个角是100°的两个等腰三角形相似
-
科目: 来源: 题型:
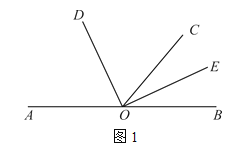
查看答案和解析>>【题目】已知,O为直线AB上一点,∠DOE=90°.
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
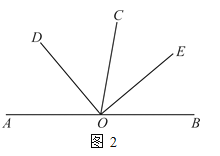
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地的实际距离为36km,用比例尺为1∶100000画在地图上的距离为__________厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是_________;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是____________.


(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使
 ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣2ax﹣4交x轴的正半轴于点A,交y轴于点B,且OA=OB.
(1)求该抛物线的解析式;
(2)若点M为AB的中点,且∠PMQ=45°,∠PMQ在AB的同侧,以点M为旋转中心将∠PMQ旋转,MP交y轴于点C,MQ交x轴于点D.设AD=m(m>0),BC=n,求n与m之间的函数关系式;
(3)在(2)的条件下,当∠PMQ的一边恰好经过该抛物线与x轴的另一个交点时,直接写出∠PMQ的另一边与x轴的交点坐标.

相关试题

