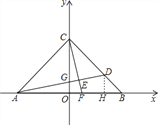
【题目】如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的![]() .
.
(1)直接写出点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.
①求证:OF=OG;(3分) ②求点F的坐标.
(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形,若存在,直接写出点P坐标;若不存在,请说明理由.

参考答案:
【答案】(1) D(4,2);(2) ①证明见解析; ②F(1.2,0); (3)存在,∴P(6,7.2),(7.2,1.2),(3.6,3.6).
【解析】分析:(1)作DH⊥AB于H,由OA=OB=OC=6,就可以得出∠ABC=45°,由三角形的面积公式就可以求出DH的值,就可以求出BH的值,从而求出D的坐标; (2)①根据OA=OC,再根据直角三角形的性质就可以得出△AOG≌△COF,就可以得出OF=OG;②由△AOG∽△AHD就可以得出OG的值,就可以求出F的坐标.(3)根据条件作出图形图1,作PH⊥OC于H,PM⊥OB于M,由△PHC≌△PMF就可以得出结论,图2,作PH⊥OB于H,由△COF≌△PHF就可以得出结论,图3,作PH⊥OC于H,由△COF≌△PHC就可以得出结论.
本题解析:
(1)作DH⊥AB于H,∴∠AHD=∠BHD=90°.∵OA=OB=OC=6,∴AB=12,
∴S△ABC=![]() =36,∵△ABD的面积为△ABC面积的
=36,∵△ABD的面积为△ABC面积的![]() .∴
.∴![]() ×36=
×36=![]() ,∴DH=2.
,∴DH=2.
∵OC=OB,∴∠BCO=∠OBC.∵∠BOC=90°,∴∠BCO=∠OBC=45°,∴∠HDB=45°,∴∠HDB=∠DBH,
∴DH=BH.∴BH=2.∴OH=4,∴D(4,2);
(2)①∵CE⊥AD,∴∠CEG=∠AEF=90°,∵∠AOC=∠COF=90°,∴∠COF=∠AEF=90°
∴∠AFC+∠FAG=90°,∠AFC+∠OCF=90°,∴∠FAG=∠OCF.
在△AOG和△COF中
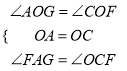 ,
,
∴△AOG≌△COF(ASA),∴OF=OG;
②∵∠AOG=∠AHD=90°,∴OG∥DH,∴△AOG∽△AHD,
∴![]() ,∴
,∴![]() ,∴OG=1.2.∴OF=1.2.∴F(1.2,0)
,∴OG=1.2.∴OF=1.2.∴F(1.2,0)
(3)如图1,当∠CPF=90°,PC=PF时,作PH⊥OC于H,PM⊥OB于M
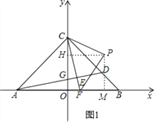
∴∠PHC=∠PHO=∠PMO=∠PMB=90°.∵∠BOC=90°,∴四边形OMPH是矩形,
∴∠HPM=90°,∴∠HPF+∠MPF=90°.∵∠CPF=90°,∴∠CPH+∠HPF=90°.
∵∠CPH=∠FPM.
在△PHC和△PMF中
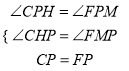 ,
,
∴△PHC≌△PMF(AAS),∴CH=FM.HP=PM,∴矩形HPMO是正方形,∴HO=MO=HP=PM.
∵CO=OB,∴COOH=OBOM,∴CH=MB,∴FM=MB.∵OF=1.2,∴FB=4.8,∴FM=2.4,
∴OM=3.6∴PM=3.6,∴P(3.6,3.6);
图2,当∠CFP=90,PF=CF时,作PH⊥OB于H,
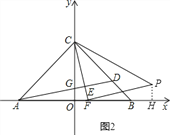
∴∠OFC+∠PFH=90,∠PHF=90,∴∠PFH+∠FPH=90,∴∠OFC=∠HPF.
∵∠COF=90,∴∠COF=∠FHP.
在△COF和△PHF中
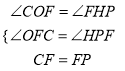 ,
,
∴△COF≌△PHF(AAS),∴OF=HP,CO=FH,∴HP=1.2,FH=6,∴OH=7.2,∴P(7.2,1.2);
图3,当∠FCP=90,PC=CF时,作PH⊥OC于H,
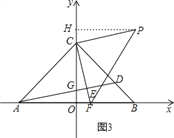
∴∠CHP=90,∴∠HCP+∠HPC=90.∵∠FCP=90,∴∠HCP+∠OCF=90,
∴∠OCF=∠HCP.∵∠FOC=90,∴∠FOC=∠CHP.
在△COF和△PHC中
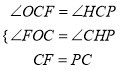 ,
,
∴△COF≌△PHC(AAS),∴OF=HC,OC=HP,∴HC=1.2,HP=6,∴HO=7.2,∴P(6,7.2),
∴P(6,7.2),(7.2,1.2),(3.6,3.6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式运算不正确的是( )
A.a3a4=a7B.(a4)4=a16
C.a5÷a3=a2D.(﹣2a2)2=﹣4a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用一个平面去截掉一个正方体的一条棱.
(1)剩下的几何体的形状是什么?
(2)剩下的几何体有几个顶点?几条棱?几个面?
(3)若按此方法截掉一个n棱柱的一条棱,则剩下的几何体有几个顶点?几条棱?几个面?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个病人每天下午要测量一次血压,下表是该病人星期一至星期六血压变化情况(“+”表示比前一天上升的部分;“-”表示比前一天下降的部分),该病人上个星期日的血压为160单位,则该病人星期五下午的血压是( )
星期
一
二
三
四
五
六
血压变化
+30
-20
+17
+18
-20
-5
A. 25单位 B. 135单位 C. 185单位 D. 190单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
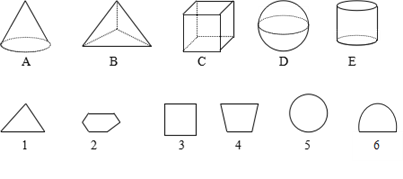
A( );B( );C( );D( );E( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】桌上倒扣着背面相同的5张扑克牌,其中3张黑桃、2张红桃.从中随机抽取一张,则( )
A.能够事先确定抽取的扑克牌的花色
B.抽到黑桃的可能性更大
C.抽到黑桃和抽到红桃的可能性一样大
D.抽到红桃的可能性更大
相关试题

