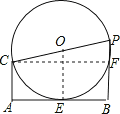
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .

参考答案:
【答案】![]() .
.
【解析】
试题分析:首先判断当AB与⊙O相切时,PB的值最大,设AB与⊙O相切于E,连接OE,则OE⊥AB,过点C作CF⊥PB于F,由CA⊥AB,DB⊥AB,得到AC∥OE∥PB,四边形ABPC是矩形,证得CF=AB=6,在直角三角形PCF中,由勾股定理列方程求解.
试题解析:当AB与⊙O相切时,PB的值最大,
如图,设AB与⊙O相切于E,连接OE,则OE⊥AB,
过点C作CF⊥PB于F,
∵CA⊥AB,DB⊥AB,
∴AC∥OE∥PB,
四边形ABPC是矩形,
∴CF=AB=6,
∵CO=OP,
∴AE=BE,
设PB=x,则PC=2OE=2+x,PF=x-2,
∴(x+2)2=(x-2)2+62,
解得;x=![]() ,
,
∴BP最大值为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经营甲、乙两种商品,其进价和售价如下表:
甲
乙
进价(元/件)
15
35
售价(元/件)
20
45
已知该商店购进了甲、乙两种商品共160件.
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,y轴上有一点A(0,1),点B是x轴上一点,∠ABO=60°,抛物线y=﹣
 x2+
x2+ +3
+3 与x轴交于C、D两点(点C在点D的左侧).
与x轴交于C、D两点(点C在点D的左侧).(1)将点C向右平移
 个单位得到点E,过点E作直线l⊥x轴,点P为y轴上一动点,过点P作PQ⊥y轴交直线l于点Q,点K为抛物线上第一象限内的一个动点,当△ABK面积最大时,求KQ+QP+PE的最小值,及此时点P的坐标;
个单位得到点E,过点E作直线l⊥x轴,点P为y轴上一动点,过点P作PQ⊥y轴交直线l于点Q,点K为抛物线上第一象限内的一个动点,当△ABK面积最大时,求KQ+QP+PE的最小值,及此时点P的坐标;(2)在(1)的条件下,将线段PE绕点P逆时针旋转90°后得线段PE′,问:在第一象限内是否存在点S,使得△SPE'是有一个角为60°,且以线段PE′为斜边的直角三角形,若存在请直接写出所有满足条件的点S,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有________.(请写出所有正确的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
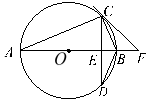
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )

A.3B.4C.5D.6
相关试题

