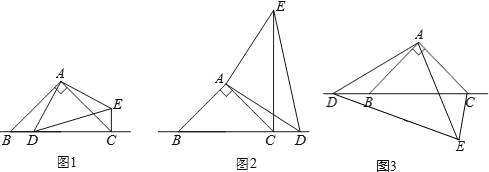
【题目】已知Rt△ABC,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,连接CE.
(1)发现问题
如图①,当点D在边BC上时,
①请写出BD和CE之间的数量关系为________,位置关系为________;
②线段CE+CD=________AC;
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中AC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;
(3)拓展延伸
如图③,当点D在边CB的延长线上且其他条件不变时,若BC=4,CE=2,求线段CD的长.
参考答案:
【答案】(1)①BD=CE,BD⊥CE;②![]() ;(2)成立,理由见解析;(3)6.
;(2)成立,理由见解析;(3)6.
【解析】
试题分析:(1)证明:如图1中,①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵AD=AE,∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中, ,∴△ABD≌△ACE,∴BD=CE,∠ABC=∠ACE=45°,∴∠ECB=90°,∴BD⊥CE;
,∴△ABD≌△ACE,∴BD=CE,∠ABC=∠ACE=45°,∴∠ECB=90°,∴BD⊥CE;

②结论:CE+CE=![]() AC.理由:由①得BD=CE,∴BC=
AC.理由:由①得BD=CE,∴BC=![]() AC,∵BC=BD+CD=CE+CD,∴CE+CD=
AC,∵BC=BD+CD=CE+CD,∴CE+CD=![]() AC;
AC;
(2)解:如图2中,存在数量关系为:CE=![]() AC+CD;
AC+CD;
理由:由(1)同理可得在△ABD与△ACE中, ,∴△ABD≌△ACE,∴BD=CE,在等腰直角三角形ABC中,BC=
,∴△ABD≌△ACE,∴BD=CE,在等腰直角三角形ABC中,BC=![]() AC,∴BD=BC+CD=
AC,∴BD=BC+CD=![]() AC+CD,∴CE=
AC+CD,∴CE=![]() AC+CD;
AC+CD;

(3)解:由(1)同理在△ABD与△ACE中, ,∴△ABD≌△ACE,∴BD=CE,∴CD=BC+BD=BC+CE.∵BC=4,CE=2,∴CD=6.
,∴△ABD≌△ACE,∴BD=CE,∴CD=BC+BD=BC+CE.∵BC=4,CE=2,∴CD=6.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次射击训练中,甲、乙两人各射击 10 次,两人 10 次射击成绩的平均数均是 8.9 环,方差分别是 S 甲2=1.7,S 乙 2=1.2,则关于甲、乙两人在这次射击训练中成绩稳定是___________.(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.必然事件的概率为1
B.数据6、4、2、2、1的平均数是3
C.数据5、2、-3、0、3的中位数是2
D.某种游戏活动的中奖率为20%,那么参加这种活动100次必有20次中奖
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的二次三项式x2﹣mx+4是完全平方式,则( )
A.m=4
B.m=﹣4
C.m=±4
D.m=±2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在义乌中小学生“我的中国梦”读书活动中,某校对部分学生作了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类。学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图如图。
“我最喜爱的图书”各类人数统计图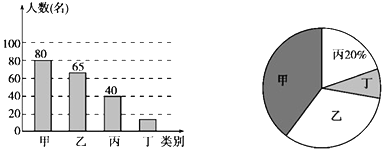
请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 名,最喜爱甲类图书的人数占本次被调查人数的 %;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500名,请你估计该校最喜爱丙类图书的女生和男生分别有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求铁架垂直管CE的长(结果精确到0.01米).
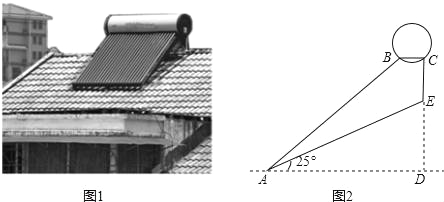
-
科目: 来源: 题型:
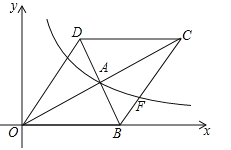
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数
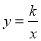 (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).(1)求反比例函数的表达式;
(2)求点F的坐标.
相关试题

