搜索
【题目】如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是 ．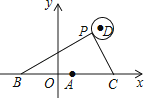 
参考答案：
【答案】6
【解析】解：∵A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），
∴AB=1﹣（1﹣a）=a，CA=a+1﹣1=a，
∴AB=AC，
∵∠BPC=90°，
∴PA=AB=AC=a，
如图延长AD交⊙D于P′，此时AP′最大，
∵A（1，0），D（4，4），
∴AD=5，
∴AP′=5+1=6，
∴a的最大值为6．
故答案为6．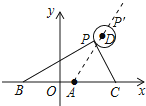
首先证明AB=AC=a，根据条件可知PA=AB=AC=a，求出⊙D上到点A的最大距离即可解决问题．本题考查圆、最值问题、直角三角形性质等知识，解题的关键是发现PA=AB=AC=a，求出点P到点A的最大距离即可解决问题，属于中考常考题型．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有一内部装有水的直圆柱形水桶，桶高20公分；另有一直圆柱形的实心铁柱，柱高30公分，直立放置于水桶底面上，水桶内的水面高度为12公分，且水桶与铁柱的底面半径比为2：1．今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为多少公分？（ ）
A.4.5
B.6
C.8
D.9 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为4的正方形ABCD内接于点O，点E是
上的一动点（不与A、B重合），点F是 
上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论，其中正确的个数是（ ）. ① 
= 
； ②△OGH是等腰三角形； ③四边形OGBH的面积随着点E位置的变化而变化；④△GBH周长的最小值为4+ 
.
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
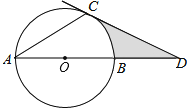
查看答案和解析>>【题目】如图，AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若∠A=∠D，CD=3，则图中阴影部分的面积为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC．
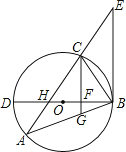
（1）求证：BE是⊙O的切线；
（2）已知CG∥EB，且CG与BD、BA分别相交于点F、G，若BGBA=48，FG=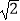
，DF=2BF，求AH的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的对角线相交于点O，点M，N分别是边BC，CD上的动点（不与点B，C，D重合），AM，AN分别交BD于点E，F，且∠MAN始终保持45°不变．
（1）求证：
= 
；
（2）求证：AF⊥FM；
（3）请探索：在∠MAN的旋转过程中，当∠BAM等于多少度时，∠FMN=∠BAM？写出你的探索结论，并加以证明． -
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=
CD，从而得出结论：AC+BC= CD．
简单应用：
（1）在图①中，若AC= ，BC=2 ，则CD= ．
（2）如图③，AB是⊙O的直径，点C、D在⊙上，
= 
，若AB=13，BC=12，求CD的长．
拓展规律：
（3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）
（4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE=
AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．
相关试题
