【题目】在直角坐标系xOy中,曲线C的参数方程为: ![]() ,以O为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
,以O为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(Ⅱ)已知直线l1: ![]() ,射线
,射线 ![]() 与曲线C的交点为P,l2与直线l1的交点为Q,求线段PQ的长.
与曲线C的交点为P,l2与直线l1的交点为Q,求线段PQ的长.
参考答案:
【答案】解:(Ⅰ)曲线C的参数方程为: 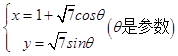 ,普通方程为(x﹣1)2+y2=7, x=ρcosθ,y=ρsinθ代入,可得曲线C的极坐标方程为ρ2﹣2ρcosθ﹣6=0;
,普通方程为(x﹣1)2+y2=7, x=ρcosθ,y=ρsinθ代入,可得曲线C的极坐标方程为ρ2﹣2ρcosθ﹣6=0;
(Ⅱ)设P(ρ1 , θ1),则有 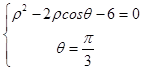 ,解得ρ1=3,θ1=
,解得ρ1=3,θ1= ![]() ,即P(3,
,即P(3, ![]() ).
).
设Q(ρ2 , θ2),则有 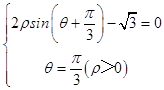 ,解得ρ2=1,θ2=
,解得ρ2=1,θ2= ![]() ,即Q(1,
,即Q(1, ![]() ),
),
所以|PQ|=|ρ1﹣ρ2|=2
【解析】(Ⅰ)把参数方程消去参数,可得曲线C的普通方程,再根据x=ρcosθ,y=ρsinθ,可得曲线C的极坐标方程.(Ⅱ)利用极坐标方程求得P、Q的坐标,可得线段PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,
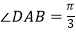 ,AB=2,AM=1,E是AB的中点.
,AB=2,AM=1,E是AB的中点. 
(1)求证:平面DEM⊥平面ABM;
(2)在线段AM上是否存在点P,使二面角P﹣EC﹣D的大小为 ?若存在,求出AP的长;若不存在,请说明理由.
?若存在,求出AP的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆C1:
 +
+  =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是  .
. 
(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx﹣
 x2(a∈R).
x2(a∈R).
(1)若x>0,恒有f(x)≤x成立,求实数a的取值范围;
(2)若函数g(x)=f(x)﹣x有两个相异极值点x1、x2 , 求证: +
+  >2ae.
>2ae. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.若a∈R,则“ <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“?x∈R,sinx+cosx≤ ”,则¬p是真命题
”,则¬p是真命题
D.命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0” -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,向量
,向量  如图表示,则( )
如图表示,则( ) 
A.?λ>0,使得
B.?λ>0,使得< ,
,  >=60°
>=60°
C.?λ<0,使得< ,
,  >=30°
>=30°
D.?λ>0,使得 为不为0的常数)
为不为0的常数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Acos2(x+φ)+1(A>0,>0,0<φ<
 )的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
)的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
A.2468
B.3501
C.4032
D.5739
相关试题

