【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)利用所探索的结论,找一组正整数a、b、m、n填空: ;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值?
)2,且a、m、n均为正整数,求a的值?
参考答案:
【答案】(1)、m2+3n2,2mn;(2)、4、2、1、1;(3)、a=22+3×12=7,或a=12+3×22=13
【解析】
试题分析:(1)、根据完全平方公式运算法则,即可得出a、b的表达式;(2)、首先确定好m、n的正整数值,然后根据(1)的结论即可求出a、b的值;(3)、根据题意,4=2mn,首先确定m、n的值,通过分析m=2,n=1或者m=1,n=2,然后即可确定好a的值.
试题解析:(1)、∵a+b![]() =
=![]() , ∴a+b
, ∴a+b![]() =m2+3n2+2mn
=m2+3n2+2mn![]() , ∴a=m2+3n2,b=2mn.
, ∴a=m2+3n2,b=2mn.
(2)、设m=1,n=1, ∴a=m2+3n2=4,b=2mn=2.
(3)、由题意,得: a=m2+3n2,b=2mn ∵4=2mn,且m、n为正整数, ∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点.
(1)求直线AC的解析式,并直接写出D点的坐标.
(2)如图1,在直线AC的上方抛物线上有一动点P,过P点作PQ垂直于x轴交AC于点Q,PM∥BD交AC于点M.
①求△PQM周长最大值;
②当△PQM周长取得最大值时,PQ与x轴交点为H,首位顺次连接P、H、O、D构成四边形,它的周长为L,若线段OH在x轴上移动,求L最小值时OH移动的距离及L的最小值.
(3)如图2,连接BD与y轴于点F,将△BOF绕点O逆时针旋转,记旋转后的三角形为△BOF′,B′F′所在直线与直线AC、直线OC分别交于点G、K,当△CGK为直角三角形时,直接写出线段BG的长.

-
科目: 来源: 题型:
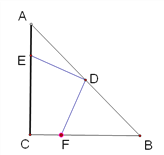
查看答案和解析>>【题目】在△ABC中,∠ACB=900,AC=BC,D为AB中点.E、F分别从A、C同时出发,以每秒1个单位速度分别向C、B运动(分别到达C、B后停止运动)
(1)求证:①DE=DF;②DE⊥DF.
(2)若AB=
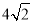 .运动时间为t.
.运动时间为t.①求△AED面积S与t的函数关系式,并写出t的取值范围;
②若△BDF为等腰三角形,求t;
③连接EF,若EF最小,求t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上星期我市某水果价格呈上升趋势,某超市第一次用1000元购进的这种水果很快卖完,第二次又用960元购进该水果,但第二次每千克的进价是第一次进价的1.2倍,购进数量比第一次少了20千克.
(1)求第一次购进这种水果每千克的进价是多少元?
(2)本星期受天气影响,批发市场这种水果的数量有所减少.该超市所购进的数量比上星期所进购的总量减少了4a%,每千克的进价在上星期第二次进价的基础上上涨5a%,结果本星期进货总额比上星期进货总额少16元,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一车间有x人,第二车间比第一车间人数的
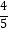 少30人,如果从第二车间调出10人到第一车间,那么:
少30人,如果从第二车间调出10人到第一车间,那么:
(1)两个车间共有多少人?
(2)调动后,第一车间的人数比第二车间多多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁从数轴上表示﹣2的点A出发,沿着数轴爬行了5个单位长度,到达点B,则点B表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,观察数轴,请回答:
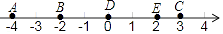
(1)点C与点D的距离为 , 点B与点D的距离为;
(2)点B与点E的距离为 , 点A与点C的距离为;
发现:在数轴上,如果点M与点N分别表示数m,n,则他们之间的距离可表示为MN= . (用m,n表示)
(3)利用发现的结论解决下列问题:数轴上表示x和2的两点P和Q之间的距离是3,则x= .
相关试题

