Question

【题目】甲，乙，丙三人各有邮票若干枚，要求互相赠送．先由甲送给乙，丙，所给的枚数等于乙，丙原来各有的邮票数；然后依同样的游戏规则再由乙送给甲，丙现有的邮票数，最后由丙送给甲，乙现有的邮票数．互相送完后，每人恰好各有64枚．你能知道他们原来各有邮票多少枚吗？说出你的思考过程．

Answer 1

【答案】解：设甲原有邮票x枚，乙原有邮票y枚，丙原有邮票z枚．

	甲	乙	丙
原有	x	y	z
第一次送后	x﹣y﹣z	2y	2z
第二次送后	2（x﹣y﹣z）	2y﹣（x﹣y﹣z）﹣2z	4z
第三次送后	4（x﹣y﹣z）	2[2y﹣（x﹣y﹣z）﹣2z]	4z﹣2（x﹣y﹣z）﹣[2y﹣（x﹣y﹣z）﹣2z]

根据第三次赠送后列方程组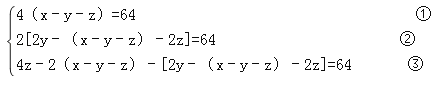
，
即 ，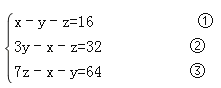
③﹣②得 2z﹣y=8 ④，
②+①得 y﹣z=24 ⑤，
④+⑤得 z=32，
将z代入⑤得 y=56，
将y、z代入①得 x=104，
答：甲原有邮票104枚，乙原有邮票56枚，丙原有邮票32枚．
【解析】假设甲原有邮票x枚，乙原有邮票y枚，丙原有邮票z枚．根据题目说明列出三次赠送的过程如下表

	甲	乙	丙
原有	x	y	z
第一次送后	x﹣y﹣z	2y	2z
第二次送后	2（x﹣y﹣z）	2y﹣（x﹣y﹣z）﹣2z	4z
第三次送后	4（x﹣y﹣z）	2[2y﹣（x﹣y﹣z）﹣2z]	4z﹣2（x﹣y﹣z）﹣[2y﹣（x﹣y﹣z）﹣2z]

根据第三次赠送后的结果列出方程组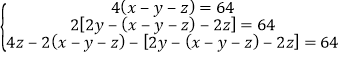
先化简，最后代入消元法或加减消元法求出方程组的解即可．
【考点精析】通过灵活运用解三元一次方程组，掌握通过“代入”或“加减”消元，把“三元”化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而转化为解一元一次方程即可以解答此题．