【题目】已知:如图,△ABC 中,AD⊥BC 于点 D,BE 是∠ABC 的平分线,若∠DAC=30°,∠BAC=80°,求:∠AOB 的度数.

参考答案:
【答案】AOB 110°.
【解析】
由AD⊥BC利用三角形内角和定理结合∠DAC=30°即可得出∠C=60°、∠ABC=40°,再根据角平分线定义可得出∠ABE=20°,在△AOB中根据三角形内角和定理即可得出∠AOB的度数.
∵ AD BC,
∴ ADC 90,
∵∠DAC 30,
∴ C 60,
∵ BAC 80 ,∠DAC 30,
∴ BAD 50,
又∵在△ABC 中, C 60 °, BAC 80 °,
∴ ABC 180 C BAC =40°,
∵BE 是∠ABC 的平分线,
∴ ABO CBO 20 °,
又∵在△ABO 中, BAO 50 °, ABO 20°,
∴ AOB 180 ABO BAO =110°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+
 x+1(a≠0)与x轴交于A,B两点,其中点B坐标为(2,0).
x+1(a≠0)与x轴交于A,B两点,其中点B坐标为(2,0).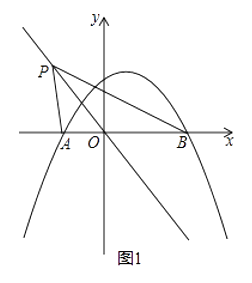
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=﹣x上的动点,当直线OP平分∠APB时,求点P的坐标;
(3)如图2,在(2)的条件下,点C是直线BP上方的抛物线上的一个动点,过点C作y轴的平行线,交直线BP于点D,点E在直线BP上,连结CE,以CD为腰的等腰△CDE的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.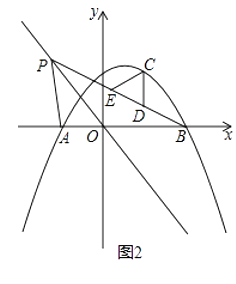
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程ax2+bx+c=0中,若a>0,b<0,c<0,则这个方程根的情况是( )
A.有两个正根
B.有两个负根
C.有一正根一负根且正根绝对值大
D.有一正根一负根且负根绝对值大 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是宽为a,长为b的长方形。用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形。
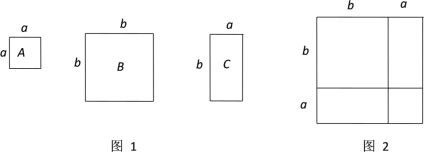
(1)请用两种不同的方式表示图2大正方形的面积。
方式1: ;
方式2: .
(2)观察图2,请你写出下列三个代数式:
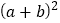 ,
,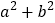 ,
,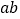 之间的等量关系。
之间的等量关系。(3)类似地,请你用图1中的三种纸片拼一个图形验证:

(4)根据(2)题中的等量关系,解决如下问题:
①已知:
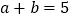 ,
,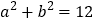 ,求
,求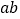 的值;
的值;②已知
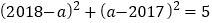 ,求
,求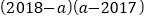 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有( )

A.2对
B.3对
C.4对
D.5对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1 是一个长为 4a、宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图 2).
(1)图 2 中的阴影部分的面积为 ;(用 a、b 的代数式表示)
(2)观察图 2 请你写出a b2 、a b2 、ab 之间的等量关系是 ;
(3)根据⑵中的结论,若 x y 5 , x y
 ,则 x y2 =_______.
,则 x y2 =_______.
相关试题

