【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)、求证:DE⊥AG;
(2)、如图2,正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°),得到正方形OE′F′G′;
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为2,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

参考答案:
【答案】(1)、证明过程见解析;(2)、①、α=30°或150°;②、最大值为4+![]() ,α=315°.
,α=315°.
【解析】
试题分析:(1)、延长ED交AG于点H,根据正方形的性质得出△AOG和△DOE全等,从而得出∠AGO=∠DEO,
根据∠AGO+∠GAO=90°得出∠GAO+∠DEO=90°,即得出垂直;(2)、①、根据∠OAG′=90°和∠OAG′=90°两种情况分别进行计算;②当α=315°时, A、O、F′在一条直线上时,AF′的长最大,最大值为4+![]() .
.
试题解析:(1)、延长ED交AG于点H, ∵点O是正方形ABCD两对角线的交点,∴OA=OD,OA⊥OD
在△AOG和△DOE中 ∴△AOG≌△DOE ∴∠AGO=∠DEO,
∴△AOG≌△DOE ∴∠AGO=∠DEO,
∵∠AGO+∠GAO=90°,∴∠GAO+∠DEO=90°,∴∠AHE=90°即DE⊥AG
(2)、①在旋转过程中,∠OAG′成为直角有两种情况:
(I):α由0°增大到90°过程中,当∠OAG′=90°时,
∵OA=OD=![]() OG=
OG=![]() OG′,∴在Rt△OAG′中,sin∠AG′O=
OG′,∴在Rt△OAG′中,sin∠AG′O=![]() =
=![]() ,∴∠AG′O=30°,
,∴∠AG′O=30°,
∵OA⊥OD,OA⊥AG′,∴OD∥AG′,∴∠DOG′=∠AG′O=30°,即α=30°;
(II):α由90°增大到180°过程中,当∠OAG′=90°时,
同理可求∠BOG′=30°,∴α=180°﹣30°=150°.
综上所述,当∠OAG′=90°时,α=30°或150°.
②当α=315°时, A、O、F′在一条直线上时,AF′的长最大,最大值为4+![]() ,α=315°.
,α=315°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )
A. 11 B. 5 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC的三边长分别为5、13、12,则△ABC的形状是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

-
科目: 来源: 题型:
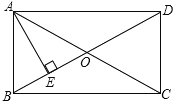
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6. (1)求∠BAE的度数;(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.1.5
B.2
C.2.5
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
(1)2x2y﹣3xy2+yx2﹣xy2
(2)2m﹣3(m﹣2n)
相关试题

