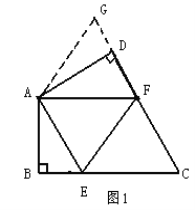
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系。
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
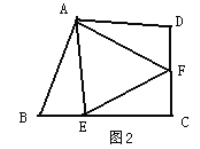
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由。
∠BAD,上述结论是否仍然成立,并说明理由。
参考答案:
【答案】(1)EF=BE+DF;EF=BE+DF仍然成立,理由见解析.
【解析】
试题分析:(1)根据全等三角形对应边相等即可得结论;(2)EF=BE+DF仍然成立,延长FD到G,使DG=BE,连接AG,根据同角的补角相等求出∠B=∠ADG,然后利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AE=AG,∠BAE=∠DAG,再求出∠EAF=∠GAF,然后利用“边角边”证明△AEF和△GAF全等,根据全等三角形对应边相等可得EF=GF,然后求解即可;
试题解析:解:(1)EF=BE+DF;
EF=BE+DF仍然成立.
证明如下:如图,延长FD到G,使DG=BE,连接AG,
∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠B=∠ADG,
在△ABE和△ADG中,
 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
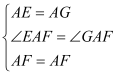 ,
,
∴△AEF≌△GAF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
-
科目: 来源: 题型:
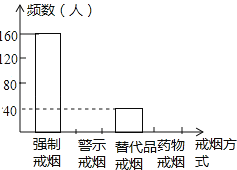
查看答案和解析>>【题目】吸烟有害健康!即使被动吸烟也大大危害健康.我国从2011年5月1日起在室内公共场合实行“禁烟令”,为配合“禁烟”行动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查,征求市民的意见,并将调查结果整理后制成了如下图表(未完成):
戒烟方式
频数
频率
强制戒烟
160
a
警示戒烟
b
0.35
替代品戒烟
40
0.1
药物戒烟
60
0.15
合计
c
1.00
根据统计图解答:
(1)填空:表中a= ,b= ,c= ;
(2)把条形统计图补充完整;
(3)如果社区有1万人,估计该地区大约有多少人支持“警示戒烟”这种方式?
-
科目: 来源: 题型:
查看答案和解析>>【题目】校文学社在全校范围内随机抽取一部分读者对社刊中最感兴趣的文学栏目进行了投票.每人一张选票,每张选票只能投给一个栏目,经统计无弃权票,根据投票结果绘制的条形统计图如下:
(1)这次参加投票的总人数为 .
(2)若全校有3000名读者,估计其中对“写作指导”最感兴趣的人数.
(3)在全校3000名读者中,若对某个栏目最感兴趣的人数少于300人将会影响社刊的销售,这个栏目就需要被撤换.请通过计算判断,“新书上架”栏目是否需要被撤换.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一轮船往返于A,B两地之间,逆水航行需3h,顺水航行需2h,水速为3km/h,则轮船的静水速度为( )
A.18km/h
B.15km/h
C.12.5km/h
D.20.5km/h -
科目: 来源: 题型:
查看答案和解析>>【题目】每年4月,安徽合肥植物园数十万株郁金香竞相怒放,吸引了众多市民前来观赏.郁金香花粉的直径约0.000000031米,这里“0.000000031”用科学记数法表示为( )
A.0.31×10-7B.3.1×10-7C.3.1×10-8D.31×10-9
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪用100元钱去购买笔记本和钢笔共15件,已知每本笔记本5元,每支钢笔7元,小聪最多能买_____支钢笔.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
相关试题

