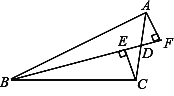
【题目】如图,已知BD为△ABC的中线,CE⊥BD于E,AF⊥BD于F.于是小白说:
“BE+BF=2BD”.你认为他的判断对吗?为什么?
参考答案:
【答案】对,理由详见解析.
【解析】试题分析:根据BD是中线得AD=CD,再根据CE⊥BD,AF⊥BD可以得到∠F=∠CED=90°,然后证明△AFD和△CED全等,再根据全等三角形对应边相等得DE=DE,再根据线段的和差关系即可证明.
试题解析:对.理由如下:
∵BD为△ABC的中线,
∴AD=CD,
∵CE⊥BD于E,AF⊥BD于F,
∴∠F=∠CED=90°,
在△AFD和△CED中,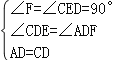 ,
,
∴△AFD≌△CED(AAS),
∴DE=DF,
∵BE+BF=(BD﹣DE)+(BD+DF),
∴BE+BF=2BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2(x﹣1)+1=0;
(2) x﹣1=
x﹣1= 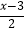 .
. -
科目: 来源: 题型:
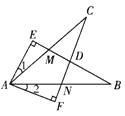
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是_______.(写出正确答案的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面里,△ABC三个顶点的坐标分别为A(﹣2,0)、B(0,3)和C(﹣3,2),若以y轴为对称轴作轴反射,△ABC在轴反射下的像是△A'B'C',则C'点坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF , 且相似比为4:3,若△ABC中BC边上的中线AM=8,则△DEF中EF边上的中线DN=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,CF∥AB.
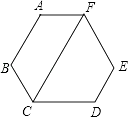
(1)求∠FCD的度数;
(2)求证:AF∥CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值是4的数是_____.平方得36的数是_____.
相关试题

