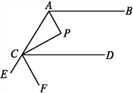
【题目】如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
参考答案:
【答案】(1)∠CAP=90°-α; (2)证明见解析;(3)证明见解析;
【解析】试题分析:(1)由角平分线的定义可得∠PAC=α,在Rt△PAC中根据直角三角形的性质可求得∠ACP;
(2)结合(1)可求得∠ACD,可证明∠ACD+∠BAC=180°,可证明AB∥CD;
(3)由平行线的性质可得∠ECF=∠CAP,∠ECD=∠CAB,结合条件可证得∠ECF=∠FCD,可证得结论.
试题解析:(1)解:∵AP平分∠BAC,∴∠CAP=∠BAP=α.
∵∠P=90°,∴∠ACP=90°-∠CAP=90°-α;
(2)证明:由(1)可知∠ACP=90°-α.
∵CP平分∠ACD,∴∠ACD=2∠ACP=180°-2α.
又∠BAC=2∠BAP=2α,∴∠ACD+∠BAC=180°,∴AB∥CD;
(3)证明:∵AP∥CF,∴∠ECF=∠CAP=α.
由(2)可知AB∥CD,∴∠ECD=∠CAB=2α,∴∠DCF=∠ECD-∠ECF=α,∴∠ECF=∠DCF,∴CF平分∠DCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据查结果,把学生的安全意识分成淡薄、一般、较强、很强四个层次,并绘制成如下两幅尚不完整的统计图:

根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为淡薄、一般的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请将条形统计图补充完整.
(3)求出安全意识为“较强”的学生所占的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知网格上最小的正方形的边长为
 (长度单位),点
(长度单位),点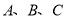 在格点上.
在格点上.(1)直接在平面直角坐标系中作出
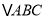 关于
关于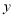 轴对称的图形
轴对称的图形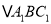 (点
(点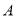 对应点
对应点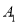 ,点
,点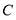 对应点
对应点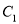 );
);(2)
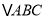 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);(3)点
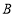 到直线
到直线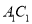 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空); 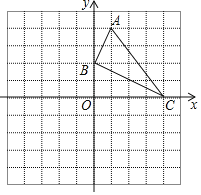
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李在某商场购买
 两种商品若干次(每次
两种商品若干次(每次 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时, 商品同时打折.三次购买
商品同时打折.三次购买 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:购买A商品的数量/个
购买B商品的数量/个
购买总费用/元
第一次
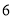
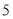

第二次


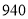
第三次
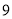
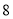

(1)求
 商品的标价各是多少元?
商品的标价各是多少元?(2)若小李第三次购买时
 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?(3)在(2)的条件下,若小李第四次购买
商品共花去了
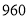 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种? -
科目: 来源: 题型:
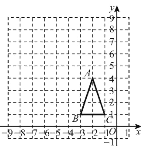
查看答案和解析>>【题目】如图,△ABC的三个顶点坐标分别为A(-2,4),B(-3,1),C(-1,1),以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A'B'C'.
(1)画出放大后的△A'B'C',并写出点A',B',C'的坐标.(点A,B,C的对应点为A',B',C')
(2)求△A'B'C'的面积.
-
科目: 来源: 题型:
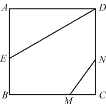
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB,CD上滑动,当CM为何值时,△AED与△CMN相似?
-
科目: 来源: 题型:
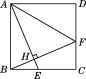
查看答案和解析>>【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.
相关试题

