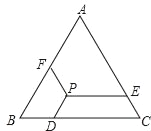
【题目】如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF等于多少,并证明你的猜想.
参考答案:
【答案】PD+PE+PF=a.理由见解析.
【解析】
延长EP交AB于G,延长FP交BC于H,然后证明△PFG和△PDH是等边三角形,根据等边三角形的性质求出PF=PG,PD=DH,再证明四边形BDPG和四边形CEPH是平行四边形,根据平行四边形的对边相等可得PG=BD,PE=CH,从而求出PD+PE+PF=BC.
解:PD+PE+PF=a.理由如下:
如图,延长EP交AB于G,延长FP交BC于H,
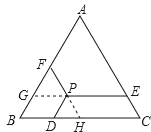
∵PE∥BC,PF∥AC,△ABC是等边三角形,
∴∠PGF=∠B=60°,∠PFG=∠A=60°,
∴△PFG是等边三角形,
同理可得△PDH是等边三角形,
∴PF=PG,PD=DH,
又∵PD∥AB,PE∥BC,
∴四边形BDPG是平行四边形,
∴PG=BD,
∴PD+PE+PF=DH+CH+BD=BC=a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2x3+32﹣32+5=(x+3)2﹣4,
∵(x+3)2≥0
∴当x=﹣3时,x2+6x+5有最小值﹣4.
请根据上述方法,解答下列问题:
(Ⅰ)x2+4x﹣1=x2+2x2+22﹣22﹣1=(x+a)2+b,则ab的值是_____;
(Ⅱ)求证:无论x取何值,代数式x2+2
 x+7的值都是正数;
x+7的值都是正数;(Ⅲ)若代数式2x2+kx+7的最小值为2,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示,直线l过点M(3,0)且平行于y轴.
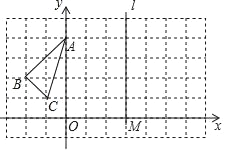
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求P1P2的长.(用含a的代数式表示)
(3)通过计算加以判断,PP2的长会不会随点P位置的变化而变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】之前我们学习了一元一次方程的解法,下面是一道解一元一次方程的题:
解方程
 ﹣
﹣ =1
=1老师说:这是一道含有分母的一元一次方程,我们可以根据等式的性质,可以把方程的两边同乘以6,这样就可以去掉分母了.于是,小明按照老师说的方法进行了解答,小明同学的解题过程如下:
解:方程两边同时乘以6,得
 ×6﹣
×6﹣ ×6=1…………①
×6=1…………①去分母,得:2(2﹣3x)﹣3(x﹣5)=1………②
去括号,得:4﹣6x﹣3x+15=1……………③
移项,得:﹣6x﹣3x=1﹣4﹣15…………④
合并同类项,得﹣9x=﹣18……………⑤
系数化1,得:x=2………………⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )
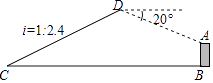
A.29.1米
B.31.9米
C.45.9米
D.95.9米 -
科目: 来源: 题型:
查看答案和解析>>【题目】若数a使关于x的不等式组
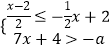 有且仅有四个整数解,且使关于y的分式方程
有且仅有四个整数解,且使关于y的分式方程 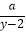 +
+ 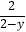 =2有非负数解,则所以满足条件的整数a的值之和是( )
=2有非负数解,则所以满足条件的整数a的值之和是( )
A.3
B.1
C.0
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为
 ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离; 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为 ,目标C的位置表示为
,目标C的位置表示为 .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )
A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
相关试题

