【题目】操作探究:
(1)实践:如图1, ![]() 中,
中,![]() 为
为![]() 边上的中线,
边上的中线,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() .则
.则![]() .
.

(2)探究:在图2中,![]() 、
、![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 、
、![]() 的中点,四边形
的中点,四边形![]() 的面积记为
的面积记为![]() ,阴影部分面积记为
,阴影部分面积记为![]() ,则
,则![]() 和
和![]() 之间满足的关系式为______:
之间满足的关系式为______:
(3)解决问题:
在图3中,![]() 、
、![]() 、
、![]() 、
、![]() 分别为任意四边形
分别为任意四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,并且图中阴影部分的面积为
的中点,并且图中阴影部分的面积为![]() 平方厘米,求图中四个小三角形的面积和,并说明理由.
平方厘米,求图中四个小三角形的面积和,并说明理由.
参考答案:
【答案】(2)S阴=![]() S四边形ABCD;(3)20,证明见解析
S四边形ABCD;(3)20,证明见解析
【解析】
(2)利用E、F分别为任意四边形ABCD的边AD、BC的中点,分别求得则S阴和S四边形ABCD即可.
(3)先设空白处面积分别为:x、y、m、n,由上得 S四边形BEDF=![]() S四边形ABCD,S四边形AHCG=
S四边形ABCD,S四边形AHCG=![]() S四边形ABCD,可得(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,然后S1+S2+S3+S4=S阴即可.
S四边形ABCD,可得(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,然后S1+S2+S3+S4=S阴即可.
(2)由E、F分别为矩形ABCD的边AD、BC的中点,
得S阴=BFCD=![]() BCCD,
BCCD,
S四边形ABCD=BCCD,
所以S阴=![]() S四边形ABCD;
S四边形ABCD;
(3)设空白处面积分别为:x、y、m、n,由题意得
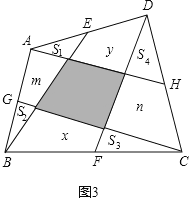
S四边形BEDF=![]() S四边形ABCD,S四边形AHCG=
S四边形ABCD,S四边形AHCG=![]() S四边形ABCD,
S四边形ABCD,
∴S1+x+S2+S3+y+S4=![]() S四边形ABCD,S1+m+S4+S2+n+S3=
S四边形ABCD,S1+m+S4+S2+n+S3=![]() S四边形ABCD,
S四边形ABCD,
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S四边形ABCD.
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,
∴S1+S2+S3+S4=S阴=20平方厘米.
故四个小三角形的面积和为20平方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比学习:
一动点沿着数轴向右平移
 个单位,再向左平移
个单位,再向左平移 个单位,相当于向右平移
个单位,相当于向右平移 个单位.用有理数加法表示为
个单位.用有理数加法表示为 .若坐标平面上的点做如下平移:沿
.若坐标平面上的点做如下平移:沿 轴方向平移的数量为
轴方向平移的数量为 (向右为正,向左为负,平移
(向右为正,向左为负,平移 个单位),沿
个单位),沿 轴方向平移的数量为
轴方向平移的数量为 (向上为正,向下为负,平移
(向上为正,向下为负,平移 个单位),则把有序数对
个单位),则把有序数对 叫做这一平移的“平移量”;“平移量”
叫做这一平移的“平移量”;“平移量” 与“平移量”
与“平移量”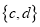 的加法运算法则为
的加法运算法则为
解决问题:
(1)计算:
 ;
;(2)动点
 从坐标原点
从坐标原点 出发,先按照“平移量”
出发,先按照“平移量” 平移到
平移到 ,再按照“平移量”
,再按照“平移量” 平移到
平移到 :若先把动点
:若先把动点 按照.“平移量”
按照.“平移量” 平移到
平移到 ,再按照“平移量”
,再按照“平移量” 平移,最后的位置还是
平移,最后的位置还是 吗?在图1中画出四边形
吗?在图1中画出四边形 .
.(3)如图2,一艘船从码头
 出发,先航行到湖心岛码头
出发,先航行到湖心岛码头 ,再从码头
,再从码头 航行到码头
航行到码头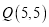 ,最后回到出发点
,最后回到出发点 .请用“平移量”加法算式表示它的航行过程.
.请用“平移量”加法算式表示它的航行过程.

解:(1)
 ______;
______;(2)答:______;
(3)加法算式:______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF是平行四边形;
(2)如果AE=3,EF=4,求AF、EC所在直线的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E,若AB=10,AC=12,求四边形CODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A=
 .(注:不要求写作法,但保留作图痕迹)
.(注:不要求写作法,但保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

相关试题

