【题目】如图，将一张矩形纸片ABCD沿对角线BD折叠，点C的对应点为C′，再将所折得的图形沿EF折叠，使得点D和点A重合．若AB=3，BC=4，则折痕EF的长为

参考答案：

【答案】
【解析】解：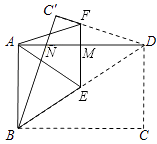
设BC′与AD交于N，EF与AD交于M，
根据折叠的性质可得：∠NBD=∠CBD，AM=DM= AD，∠FMD=∠EMD=90°，
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC=4，∠BAD=90°，
∴∠ADB=∠CBD，
∴∠NBD=∠ADB，
∴BN=DN，
设AN=x，则BN=DN=4﹣x，
∵在Rt△ABN中，AB2+AN2=BN2 ，
∴32+x2=（4﹣x）2 ，
∴x= ，
即AN= ，
∵C′D=CD=AB=3，∠BAD=∠C′=90°，∠ANB=∠C′ND，
∴△ANB≌△C′ND（AAS），
∴∠FDM=∠ABN，
∴tan∠FDM=tan∠ABN，
∴ ，
∴ ，
∴MF= ，
由折叠的性质可得：EF⊥AD，
∴EF∥AB，
∵AM=DM，
∴ME= AB= ，
∴EF=ME+MF= + = ．
所以答案是： ．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．

关闭