【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2 ![]() ,若∠EOF=45°,则F点的纵坐标是 ( )
,若∠EOF=45°,则F点的纵坐标是 ( )
A.![]()
B.1
C.![]()
D.![]()
-1
参考答案:
【答案】A
【解析】解:如图连接EF,延长BA使得AM=CE,则△OCE≌△OAM.
∴OE=OM,∠COE=∠MOA,
∵∠EOF=45°,
∴∠COE+∠AOF=45°,
∴∠MOA+∠AOF=45°,
∴∠EOF=∠MOF,
在△OFE和△OFM中,
|
∴△OFE≌△FOM,
∴EF=FM=AF+AM=AF+CE,设AF=x,
∵CE=![]()
∴EF=2+x,EB=2,FB=4-x,
∴(2+x)2=22+(4-x)2 ,
∴x=![]() ,
,
∴点F的纵坐标为![]() ,
,
故选A.
根据∠EOF==∠COE+∠AOF=45°,构造△OFE≌△FOM,如图,再运用勾股定理构造方程解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x-2)2+3的对称轴是( )
A.直线x=3B.直线x=-3C.直线x=-2D.直线x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
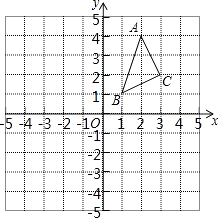
(1)画出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;
(2)画出△ABC关于y轴对称的△A2B2C2 , 并写出点B2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(﹣2,y1),B(﹣1,y2),C(8,y3)都在二次函数y=ax2(a<0)的图象上,则下列结论正确的是( )
A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】货主两次租用某汽车运输公司的甲,乙两种货车运送货物往某地,第一次租用甲货车2辆和乙货车3辆共运送15.5吨货物,第二次租用甲货车3辆和乙货车2辆共运送17吨货物,两次运输都按货车的最大核定载货量刚好将货物运送完,没有超载.
(1)求甲,乙两种货车每辆最大核定载货量是多少吨?
(2)已知租用甲种货车运费为每辆1200元,租用乙种货车运费为每辆800元,现在货主有24吨货物需要运送,而汽车运输公司只有2辆甲种货车,其它的都是乙种货车,问有几种租车方案?哪种方案费用较少? -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O , A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点
C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点Bn的坐标是 .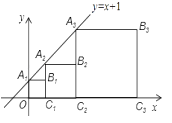
相关试题

