搜索
【题目】计算：(1) 
；(2) 
；
(3)
；(4) 
参考答案：
【答案】（1）－3；（2）
；（3）
；（4）
【解析】
有理数的加减混合运算，可以利用加法的运算律将负数与正数分开分别相加，这样可以减少异号两数相加易犯的错误，整式加减运算先去括号，然后合并同类项即可.
解：（1）原式=6—0.5—10＋1.5=（6－10）＋（－0.5＋1.5）=－4＋1=－3；
（2）原式=－3－
＋4 =（－3＋4）－ =1－ =；
(3)原式=
=
=
=
；
(4)原式=
=
.
“点睛”本题在运算过程中第一步是将加减统一成加法，第二步是省略加号写成代数和的形式，第三步是运用了加法交换律，第四步是运用了加法结合律，后面是利用加法法则，通过运算过程我们还可以看到加法的运算律在运算中的重要作用.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AB＝AC，点D在底边BC上，添加下列条件后，仍无法判定△ABD≌△ACD的是( )
A. BD＝CD B. ∠BAD＝∠CAD C. ∠B＝∠C D. ∠ADB＝∠ADC
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm，求CM和AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是（ ）
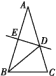
A. BD平分∠ABC B. D是AC的中点
C. AD=BD=BC D. △BDC的周长等于AB+BC
-
科目： 来源： 题型：
查看答案和解析>>【题目】填空并在括号内加注理由。
如图，已知
∥
，
、
分别平分
和
求证：
证明：∵
∥∴
= （ ） ∵
、平分、∴
=
∴
= （ ）∴
=∴ ∥ ( )
∴
=∠ （ ） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在线段AB上取一点C(非中点)，分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE，连接AE交CD于F，连接BD交CE于G，AE和BD交于点H，则下列结论：①AE＝DB；②不另外添加线，图中全等三角形只有1对；③若连接FG，则△CFG是等边三角形；④若连接CH，则CH平分∠FHG.其中正确的是________(填序号)．
-
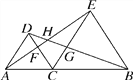
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．
（1）当D点在BC的什么位置时，DE=DF？请说明理由．
（2）DE，DF，CG的长之间存在着怎样的等量关系？并说明理由.
（3）若D在底边BC的延长线上，（2）中的结论还成立吗？若不成立，又存在怎样的关系？并说明理由.
相关试题
