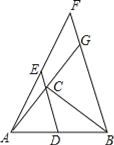
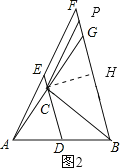
【题目】如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=![]() CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AB=BG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.
参考答案:
【答案】(1)证明见解析;(2)当PB=2.5或![]() 时,△BCP与△BCD相似.
时,△BCP与△BCD相似.
【解析】试题分析:(1)利用平行分线段成比例定理得出![]() ,进而得出△ABC≌△GBC(SAS),即可得出答案;
,进而得出△ABC≌△GBC(SAS),即可得出答案;
(2)分别利用第一种情况:若∠CDB=∠CPB,第二种情况:若∠PCB=∠CDB,进而求出相似三角形即可得出答案.
试题解析:(1)证明:∵BF∥DE,
∴![]() ,
,
∵AD=BD,
∴AC=CG,AE=EF,
在△ABC和△GBC中:
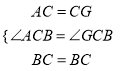 ,
,
∴△ABC≌△GBC(SAS),
∴AB=BG;
(2)当BP长为![]() 或
或![]() 时,△BCP与△BCD相似;
时,△BCP与△BCD相似;
∵AC=3,BC=4,
∴AB=5,
∴CD=2.5,
∴∠DCB=∠DBC,
∵DE∥BF,
∴∠DCB=∠CBP,
∴∠DBC=∠CBP,
第一种情况:若∠CDB=∠CPB,如图1:
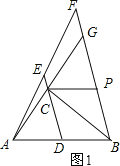
在△BCP与△BCD中
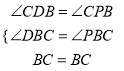 ,
,
∴△BCP≌△BCD(AAS),
∴BP=CD=2.5;
第二种情况:若∠PCB=∠CDB,过C点作CH⊥BG于H点.如图2:
∵∠CBD=∠CBP,
∴△BPC∽△BCD,
∵CH⊥BG,
∴∠ACB=∠CHB=90°,∠ABC=∠CBH,
∴△ABC∽△CBH,
∴![]() ,
,
∴BH=![]() ,BP=
,BP=![]() .
.
综上所述:当PB=2.5或![]() 时,△BCP与△BCD相似.
时,△BCP与△BCD相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)若∠DBC=25°,求∠ADC′的度数;
(2)若AB=4,AD=8,求△BDE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
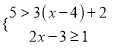 .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法.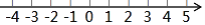
(1)解不等式(1),得________;
(2)解不等式(2),得________;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:

解:因为AD∥BC(已知),
所以∠1=∠3( ).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥________( ).
所以∠3+∠4=180°( ).
-
科目: 来源: 题型:
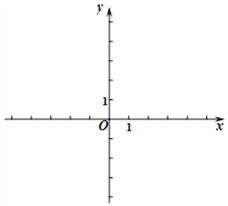
查看答案和解析>>【题目】已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
相关试题

