【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
例如:①用配方法解题如下: ![]()
原式=![]() +6x+9+1=
+6x+9+1=![]()
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是0+1=1;所以当
的最小值是0+1=1;所以当![]() 时,原多项式的最小值是1.
时,原多项式的最小值是1.
请根据上面的解题思路,探求:
(1)若(x+1)2+(y-2)2=0,则x= ,y= ..
(2)若x2+y2+6x-4y+13=0,求x,y的值;
(3)求![]() 的最小值
的最小值
参考答案:
【答案】(1)x=-1,y=2;(2)x=-3,y=2;(3)最小值为-6
【解析】试题分析:利用非负数的性质求出最小值,以及此时![]() 的值即可.
的值即可.
试题解析:(1)∵![]()
![]()
解得![]()
![]()
![]()
则![]()
解得![]()
(3)![]()
最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.
 B.
B.  C.
C.  D.
D. 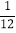
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.

⑴ 求证:AB=AC.
⑵ 若BD=11,DE=2,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)降价前每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
-
科目: 来源: 题型:
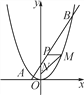
查看答案和解析>>【题目】如图,已知一条直线过点(0,4),且与抛物线y=
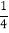 x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量
 (万件)与销售单价
(万件)与销售单价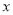 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数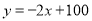 (利润=售价﹣制造成本)
(利润=售价﹣制造成本)(1)写出每月的利润
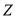 (万元)与销售单价
(万元)与销售单价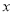 (元)之间的函数关系式;
(元)之间的函数关系式;(2)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
相关试题

