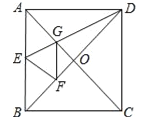
【题目】如图，正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连结GF，给出下列结论：①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是，其中正确的结论个数为（ ）

A．2 B．3 C．4 D．5

参考答案：

【答案】B．

【解析】

试题分析：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG=∠ADO=22.5°，故①正确．

∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴＞2，故②错误．

∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD＞S△OGD，故③错误．

∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．

∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF=OG，∴BE=EF=×OG=2OG．

故⑤正确．

∵四边形AEFG是菱形，∴AB∥GF，AB=GF．

∵∠BAO=45°，∠GOF=90°，∴△OGF时等腰直角三角形．

∵S△OGF=1，∴=1，解得OG=，∴BE=2OG=，GF===2，∴AE=GF=2，∴AB=BE+AE=，∴S正方形ABCD===，故⑥错误，∴其中正确结论的序号是：①④⑤．

故选B．

关闭