【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
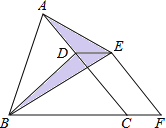
A.3 B.4 C.6 D.8
参考答案:
【答案】D
【解析】
试题分析:连接EC,过A作AM∥BC交FE的延长线于M,求出平行四边形ACFM,根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,推出阴影部分的面积等于平行四边形ACFM的面积的一半,求出CF×hCF的值即可.
解:连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
同理△ADE的面积和△AME的面积相等,
即阴影部分的面积等于平行四边形ACFM的面积的一半,是![]() ×CF×hCF,
×CF×hCF,
∵△ABC的面积是24,BC=3CF
∴![]() BC×hBC=
BC×hBC=![]() ×3CF×hCF=24,
×3CF×hCF=24,
∴CF×hCF=16,
∴阴影部分的面积是![]() ×16=8,
×16=8,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,-5)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200×2x=1000
C.200+200×3x=1000
D.200[1+(1+x)+(1+x)2]=1000
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连结OA,二次函数y=x2图象从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
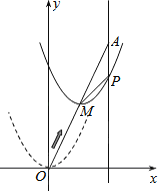
(1)求线段OA所在直线的函数解析式;
(2)设二次函数顶点M的横坐标为m,当m为何值时,线段PB最短,并求出二次函数的表达式;
(3)当线段PB最短时,二次函数的图象是否过点Q(a,a﹣1),并说理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个内角等于150°,则这个正多边形的边数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个外角是40°,则这个正多边形是( )
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1,(a,m,b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是 .
相关试题

