【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
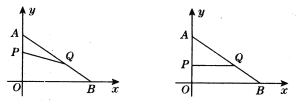
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
参考答案:
【答案】(1)![]() (2)3 (3)10
(2)3 (3)10
【解析】
试题分析:(1)设直线AB的解析式y=kx+b; 已知点A(0,6)、点B(8,0),则![]() ;解得
;解得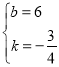 ,所以直线AB的解析式为
,所以直线AB的解析式为![]()
(2)如果丙的第二句话是正确的,那么根据抛物线的对称性可知,此抛物线的对称轴是直线x=2,这样甲的第一句和乙的第一句就都错了,这样又和(1)中的判断相矛盾,所以乙的第二句话也是错的;根据老师的意见,丙的第三句也就是错的.也就是说,这条抛物线一定过点(-1,0); 6分
(3)由甲乙的第一句话可以断定,抛物线的对称轴是直线x=1,抛物线经过(-1,0),那么抛物线与x轴的两个交点间的距离为4,所以乙的第三句话是错的;
由上面的判断可知,此抛物线的顶点为(1,-8),且经过点(-1,0)
设抛物线的解析式为:y=a(x-1)![]() -8
-8
∵抛物线过点(-1,0)
∴0=a(-1-1)![]() -8
-8
解得:a=2
∴抛物线的解析式为y=2(x-1)![]() -8
-8
即:y=2x![]() -4x-6 12分
-4x-6 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣2a2(a﹣3ab)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣a2)3=( )
A. a6B. ﹣a6C. a5D. ﹣a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.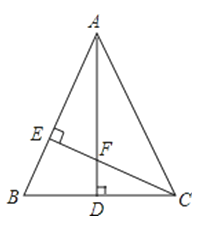
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.
结论1:DM、MN的数量关系是 ;
结论2:DM、MN的位置关系是 ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
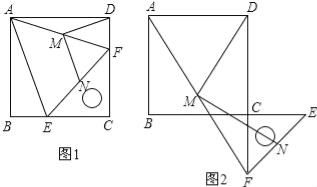
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的外角和是内角和的一半,则它是( )边形 ( )
A.7 B.6 C.5 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形最少可分割成五个三角形,则它是( )边形
A. 8 B. 7 C. 6 D. 5
相关试题

