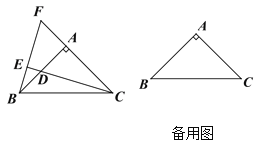
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。
参考答案:
【答案】(1)AB=AF+BD,证明详见解析;(2)不成立,点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF,证明详见解析.
【解析】
(1)根据已知条件易证△FAB≌△DAC,由全等三角形的性质可得FA=DA,由此即可证得AB=AD+BD=FA+BD;(2)由于点D的位置在变化,因此线段AF、BD、AB之间的大小关系也会相应地发生变化,只需画出图象并借鉴(1)中的证明思路就可解决问题.
(1)AB=FA+BD.
证明:如图,
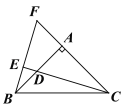
∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,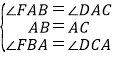 .
.
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
点D在AB的延长线上时,如图2.
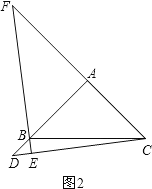
类比(1)的方法可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.

类比(1)的方法可得:FA=DA.
则AB=BD-AD=BD-AF.
-
科目: 来源: 题型:
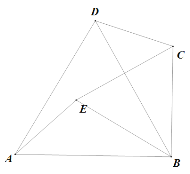
查看答案和解析>>【题目】如图:两个等边三角形△ABD与△BCE,连结AE与CD,
求证:(1)AE=CD;
(2)AE与DC之间的夹角为60°;
(3)AE与CD的交点设为H,BH平分∠AHC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校办工厂现在年产值是15万元,计划以后每年增加2万元.
(1)写出年产值
 (万元)与年数
(万元)与年数 之间的关系式.
之间的关系式.(2)用表格表示当
 从0变化到6(每次增加1)
从0变化到6(每次增加1) 的对应值.
的对应值.(3)求5年后的年产值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
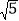 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+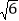 .其中正确结论的序号是( )
.其中正确结论的序号是( )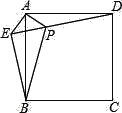
A. ①②③ B. ①②④ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子
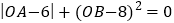
(1)求A,B两点的坐标;
(2)若点O到AB的距离为
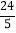 ,求线段AB的长;
,求线段AB的长;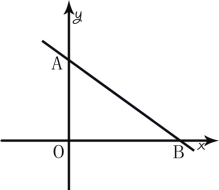
(3)在(2)的条件下,x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形,若存在请直接写出满足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是_____.
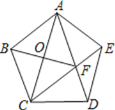
相关试题

