搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于点D，P是 
上的一个动点，连接AP，则AP的最小值是 ． 
参考答案：
【答案】
﹣1
【解析】解：找到BC的中点E，连接AE，交半圆于P2，在半圆上取P1，连接AP1，EP1，
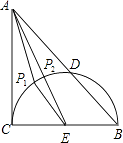
可见，AP1+EP1＞AE，
即AP2是AP的最小值，
∵AE= 
= ，P2E=1，
∴AP2= ﹣1．
所以答案是： ﹣1．
【考点精析】本题主要考查了等腰直角三角形和线段的基本性质的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD⊥BC于D，EG⊥BC于G，∠E＝∠1，可得AD平分∠BAC．
理由如下：∵AD⊥BC于D，EG⊥BC于G，（_______）
∴∠ADC＝∠EGC＝90°，（垂直的定义），
∴AD∥EG，（_______）
∴∠1＝∠2，（_______）
∠E＝∠3，（_______）
又∵∠E＝∠1（已知），
∴______＝_______，（______）
∴AD平分∠BAC．（_______）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知某的士的起步价为10元（可以坐3千米的路程），若超过3千米，则超出部分每千米另外加收2 元.
（1）小明坐该的士走了x千米的路程，应该付费多少元？
（2）小芳坐该的士走了18千米的路程，应该付费多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A在数轴上对应的数为a，点B在数轴上对应的数为b，且|a+3|+|b-2|=0，A,B 之间的距离记为|AB|.请回答问题：
(1)直接写出a,b, |AB|的值. a= ，b = ， |AB|= ；
(2)设点P在数轴上对应的数为x，当|PA|-|PB|=2时，求x的值；
(3)若点P在点A的左侧，M、N分别是PA、PB的中点.当点P在点A的左侧移动时，式子|PN|-|PM|的值是否发生改变？若不变，请求出其值；若发生变化，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】点A、B在数轴上分别表示实数
、
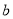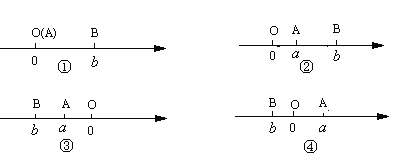
，A、B两点之间的距离记作AB.当A、B两点中有一点为原点时，不妨设A点在原点.如图①所示，则AB＝OB＝
＝
．
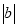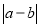当A、B两点都不在原点时：
(1)如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB－OA＝
＝
＝
＝
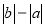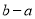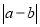
(2)如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB－OA＝
＝
＝
＝
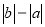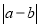
(3)如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB＋OA＝
＝
＝
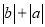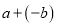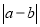
回答下列问题：
(1)综上所述，数轴上A、B两点之间的距离AB＝ ．
(2)数轴上表示2和－4的两点A和B之间的距离AB＝ ．
(3)数轴上表示
和－2的两点A和B之间的距离AB＝ ，如果AB＝2，则
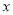的值为 ．(4)若代数式
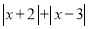有最小值，则最小值为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，Rt△ABC的顶点B在原点O，直角边BC在x轴的正半轴上，∠ACB=90°，点A的坐标为（3，
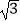），点D是BC边上一个动点（不与点B，C重合），过点D作DE⊥BC交AB边于点E，将∠ABC沿直线DE翻折，点B落在x轴上的点F处当△AEF为直角三角形时，点F的坐标是 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，则∠EBC等于（ ）
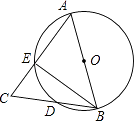
A.22.5°
B.23°
C.25°
D.30°
相关试题
