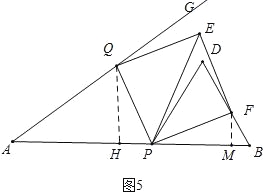
【题目】如图,tan∠GAB=![]() ,AB=10cm,点P从点B出发以5cm/s的速度沿BA向终点A运动,同时点Q以相同的速度从点A出发沿射线AG运动,分别以PB、PQ为边作等边△BPD,正方形PQEF,连接PE,设运动的时间为ts.
,AB=10cm,点P从点B出发以5cm/s的速度沿BA向终点A运动,同时点Q以相同的速度从点A出发沿射线AG运动,分别以PB、PQ为边作等边△BPD,正方形PQEF,连接PE,设运动的时间为ts.
(1)当PE⊥AG时,求t的值;
(2)当△APQ是等腰三角形时,求t的值;
(3)当点F落在△BPD的边上时,请直接写出t的值.

参考答案:
【答案】(1)t=![]() .(2)当△APQ是等腰三角形时,t的值为1s,
.(2)当△APQ是等腰三角形时,t的值为1s,![]() s,
s,![]() s.
s.
(3)t=![]() s或
s或![]() s时,点F落在△BPD的边上.
s时,点F落在△BPD的边上.
【解析】
试题分析:(1)如图1,设PE交AG于点M,过点Q作QN⊥AP于N,在RT△ANQ中,tan∠GAB=![]() ,设QN=3k,AN=4k,则AQ=5k,列出方程即可角问题.
,设QN=3k,AN=4k,则AQ=5k,列出方程即可角问题.
(2)如图2中,过点Q作QH⊥AP于H,分三种情形①当AQ=AP时,②当AP=PQ时,③当AQ=PQ时,列出方程即可.
(3))①如图3中,当点F在直线PD上时,作QH⊥AB于H,②如图4中,当点F在直线PB上时,③如图5中,当点F在BD边上时,作QH⊥AB于H,FM⊥AB于M.
分别列出方程即可解决问题.
试题解析:(1)如图1,设PE交AG于点M.
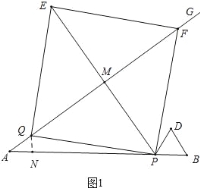
∵四边形PQEF是正方形,∴PE⊥FQ,∴当PE⊥AG时,点F在AG上,∴PM=MQ,
过点Q作QN⊥AP于N,在RT△ANQ中,tan∠GAB=![]() ,设QN=3k,AN=4k,则AQ=5k,
,设QN=3k,AN=4k,则AQ=5k,
∴sin∠MAP=![]() ,cos∠MAP=
,cos∠MAP=![]() ,∵AP=10﹣5t,
,∵AP=10﹣5t,
∴MQ═PM=APsin∠MAP=6﹣3t,AM=APcos∠MAP=8﹣4t,
∵AQ=5t,∴5t+(6﹣3t)=8﹣4t,
∴t=![]() .
.
(2)如图2中,过点Q作QH⊥AP于H,
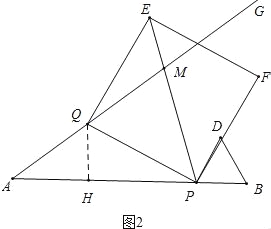
在RT△AQH中,AQ=5t,
∴AH=AQsin∠MAP=5t![]() =4t,QH=AQsin∠MAP=3t,
=4t,QH=AQsin∠MAP=3t,
∵AP=10﹣5t,
∴HP=10﹣9t,
在RT△PQH中,∵∠PHQ=90°,
∴PQ2=HQ2+PH2=(10﹣9t)2+(3t)2=90t2﹣180t+100,
①当AQ=AP时,10﹣5t=5t,解得t=1,
②当AP=PQ时,(10﹣5t)2=90t2﹣180t+100,解得t=![]() (或0舍弃),
(或0舍弃),
③当AQ=PQ时,10﹣5t=3t,解得t=![]() ,
,
综上所述,当△APQ是等腰三角形时,t的值为1s,![]() s,
s,![]() s.
s.
(3)①如图3中,当点F在直线PD上时,作QH⊥AB于H,
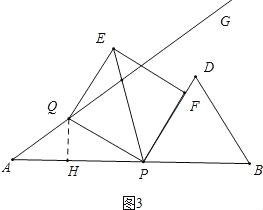
∵∠QOH+∠DPB=90°,∠DPB=60°,
∴∠QPH=30°,
∴PF=PQ=2QH=6t
∴PF>PD,
这种情形不符合题意.
②如图4中,当点F在直线PB上时,
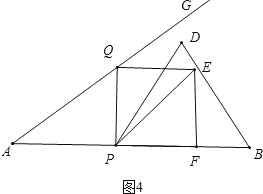
在RT△AQP中,∵AQ=5t.AP=4t,
又∵AP=10﹣5t,
∴4t=10﹣5t,
∴t=![]() ,此时PQ=4t<5t,符合题意.
,此时PQ=4t<5t,符合题意.
③如图5中,当点F在BD边上时,作QH⊥AB于H,FM⊥AB于M.
由△QPH≌△PFM,得到QH=PM=3t,HP=FN=10﹣5t﹣4t=10﹣9t,
在RT△FNB中,∵∠B=60°,
∴BM=![]() FM=
FM=![]() (10﹣9t),
(10﹣9t),
∵PM+BM=PB,
∴3t+![]() (10﹣9t)=5t,
(10﹣9t)=5t,
∴t=![]() .
.
综上所述t=![]() s或
s或![]() s时,点F落在△BPD的边上.
s时,点F落在△BPD的边上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
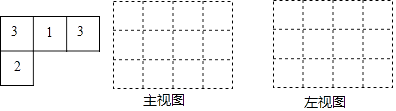
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加块小正方体. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC.
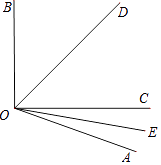
(1)求∠EOD的度数.
(2)若∠BOC=90°,求∠AOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云: 今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有.
注:古代一斗是10升.
大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.
(1)列方程求壶中原有多少升酒;
(2)设壶中原有a0升酒,在第n个店饮酒后壶中余an升酒,如第一次饮后所余酒为a1=2a0﹣5(升),第二次饮后所余酒为a2=2a1﹣5=22a0﹣(22﹣1)×5(升),… 用含an﹣1的式子表示an= , 再用含a0和n的式子表示an=;
(3)按照这个约定,如果在第4个店喝光了壶中酒,请借助①中的结论求壶中原有多少升酒. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人参加射击比赛,每人各射击10次,两人所得环数的平均数相同,其中甲所得环数的方差为15,乙所得环数的方差为18,那么成绩较为稳定的是______(填“甲”或“乙”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,A,B为数轴上两点,AB=15,且OA:OB=2.

(1)A,B对应的数分别为、;
(2)点A,B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A、B相距1个单位长度?
(3)点A,B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OB﹣mOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件.
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?(列方程组解答)
(2)若加工童装一件可获利25元,加工成人装一件可获利50元,那么该车间加工完这批服装后,共可获利多少元?
相关试题

