【题目】如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为 
参考答案:
【答案】![]()
【解析】解:如图:
设正方形ABCD的边长为a,则AB=BC=AD=a,
∵四边形ABCD是正方形,
∴∠ABC=90°,AD∥BC,OD=OB,
由勾股定理得:AC=![]() a,
a,
延长FP交AD于M,过B作BN∥AC交AF的延长线于N,
则∠N=∠CAF,
∵AF平分∠BAC,
∴∠BAF=∠CAF,
∴∠N=∠BAF,
∴AB=BN=a,
∵BN∥AC,
∴△NFB∽△AFC,
∴BF=(![]() ﹣1)a,
﹣1)a,
∴CF=a﹣(![]() ﹣1)a=(2﹣
﹣1)a=(2﹣![]() )a,
)a,
∵AD∥BC,
∴△BOF∽△DOM,![]()
∵OD=OB,
∴DM=BF=(![]() ﹣1)a,
﹣1)a,
∵点G是AD的中点,
∴DG=AG=![]() a,
a,
∴GM=![]() a﹣(
a﹣(![]() ﹣1)a=(
﹣1)a=(![]() -
-![]() )a,
)a,
∵AD∥BC,
∴△GMP∽△CFP,
所以答案是:![]() .
. 
【考点精析】本题主要考查了角平分线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A.y=(x﹣1)2+2
B.y=(x﹣2)2+4
C.y=(x﹣2)2+2
D.y=(x﹣1)2+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】温州文化用品市场A商家独家销售某种儿童玩具,每件进价为40元.经过市场调查,一周的销售量
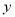 件与销售单价
件与销售单价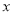 (
(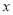 ≥45)元/件的关系如下表:
≥45)元/件的关系如下表:销售单价
 (元/件)
(元/件)…
45
55
70
75
…
一周的销售量
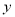 (件)
(件)…
550
450
300
250
…
(1)直接写出
 与
与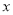 的函数关系式: ;
的函数关系式: ;(2)设一周的销售利润为W元,请求出W与
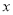 的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润(W)随着销售单价(
的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润(W)随着销售单价(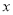 )的增大而增大?
)的增大而增大?(3)A商家决定将该玩具一周的销售利润全部捐给孤儿院,在商家购进该商品的钱款数额不超过8000元的情况下,请你求出该商家最大捐款数额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 和
和 都是关于x、y的方程y=kx+b的解.
都是关于x、y的方程y=kx+b的解.
(1)求k、b的值
(2)若不等式3+2x>m+3x的最大整数解是k,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OE,OD分别平分∠AOC和∠BOC.
(1)如果∠AOB=900,∠BOC=400,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β (α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律.

相关试题

