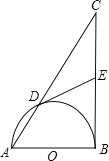
【题目】如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.
参考答案:
【答案】见解析
【解析】
试题分析:先连接OD和BD,根据圆周角定理求出∠ADB=90°,根据直角三角形斜边上中线性质求出DE=BE,推出∠EDB=∠EBD,∠ODB=∠OBD,即可求出∠ODE=90°,根据切线的判定推出即可.
证明:连接OD,BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BDC=90°,
∵E为BC的中点,
∴DE=BE=CE,
∴∠EDB=∠EBD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BC切⊙O于点B,
∴∠ABC=90°,
∴∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=∠ABC=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形
B.矩形的对角线相等且互相平分
C.对角线互相平分的四边形是矩形
D.矩形的对角线互相垂直且平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是1440°,且这个多边形的每一个内角都相等,则这个多边形的一个外角是( )
A. 60° B. 45° C. 36° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在4×4的方格中有五个同样大小的正方形如图1摆放,移动其中一个正方形到空白方格中,与其余四个正方形图2至图5组成的新图形是一个轴对称图形,请在下面网格中画出四种互不全等的新图形.

(2)定义:如图1,点M,N把线段AB分割成AM,MN和BN.若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一个点D,使点C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);

-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年,深圳市人居环境委通报了2014年深圳市大气PM2.5来源研究成果.报告显示主要来源有,A:机动车尾气,B:工业VOC转化及其他工业过程,C:扬尘,D:远洋船,E:电厂,F:其它.某教学学习小组根据这些数据绘制出了如下两幅尚不完整的统计图(图1,图2).
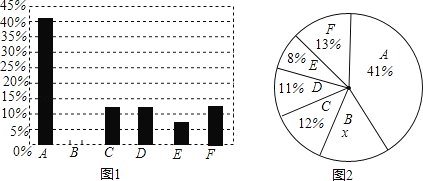
请你根据统计图中所提供的信息解答下列问题:
(1)图2的扇形统计图中,x的值是 ;
(2)请补全图1中的条形统计图;
(3)图2的扇形统计图中,“A:机动车尾气”所在扇形的圆心角度数为 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的直径.
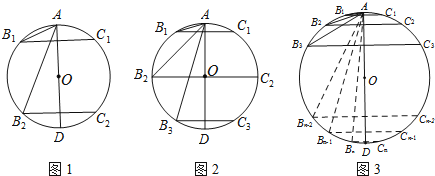
(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是 ;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是 (用含n的代数式表示∠Bn的度数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点A(m ,-2)、B(1,n-m)关于x轴对称,则m、n的值为( )
A. m =1 ,n=1 B. m =-1 ,n=1 C. m =1 ,n=3 D. m =-1 ,n=3
相关试题

