搜索
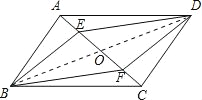
【题目】（6分）如图，四边形ABCD是平行四边形，E、F是对角线AC上的两点，AF=EC，求证：四边形EBFD是平行四边形．
参考答案：
【答案】见解析
【解析】首先连接BD，交AC于点O，由四边形ABCD是平行四边形，根据平行四边形的对角线互相平分，即可求得OA=OC，OB=OD，又由AF=EC，可得OE=OF，然后根据对角线互相平分的四边形是平行四边形．
证明：连接BD，交AC于点O，
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵AF=EC，
∴AF﹣OA=EC﹣OC，
即OE=OF，
∴四边形EBFD是平行四边形．
“点睛”本题考查了平行四边的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把多项式中各项的提取出来,写成公因式与另一个因式的的形式,这种因式分解的方法叫做提公因式法.
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：2x2+y2+（2y2﹣3x2）﹣2（y2﹣2x2），其中x=﹣1，y=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法：
解：∵x﹣y=2，又∵x＞1，∴y+2＞1，即y＞﹣1
又y＜0，∴﹣1＜y＜0．…①
同理得：1＜x＜2．…②
由①+②得﹣1+1＜y+x＜0+2，∴x+y的取值范围是0＜x+y＜2．
请按照上述方法，完成下列问题：
已知关于x、y的方程组
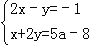的解都为非负数．（1）求a的取值范围；
（2）已知2a﹣b=1，且，求a+b的取值范围；
（3）已知a﹣b=m（m是大于1的常数），且b≤1，求2a+b最大值．（用含m的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】（15分）解下列方程：
（1）4x－3（12－x）＝6x－2（8－x）；
（2）
；（3）
． -
科目： 来源： 题型：
查看答案和解析>>【题目】用科学记数法表示2030000，应记作 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（12分）把正整数1，2，3，4，…，2017排列成如图所示的一个数表．
（1）用一正方形在表中随意框住4个数，把其中最小的数记为x，另三个数用含x的式子表示出来，从大到小依次是 ， ， ；
（2）当被框住的4个数之和等于416时，x的值是多少？
（3）被框住的4个数之和能否等于622？如果能，请求出此时x的值；如果不能，请说明理由．
相关试题
