【题目】已知:如图,等腰梯形ABCD的中位线EF的长为6cm,对角线BD平分∠ADC,下底BC的长比等腰梯形的周长小20cm,求上底AD的长.

参考答案:
【答案】4cm.
【解析】由等腰梯形的性质得出AB=DC,AD∥BC,得出∠ADB=∠CBD,再由已知条件得出BC=DC=AB,由梯形中位线定理得出AD+BC=2EF=12cm,由已知条件求出BC,即可得出AD的长.
解:∵四边形ABCD是等腰梯形,
∴AB=DC,AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ADC,
∴∠ADB=∠CDB,
∴∠CBD=∠CDB,
∴BC=DC=AB,
∵EF是等腰梯形的中位线,
∴AD+BC=2EF=12cm,
∵下底BC的长比等腰梯形的周长小20cm,
∴BC=AB+BC+CD+AD﹣20,
即BC=AB+DC﹣8,
∴BC=8cm,
∴AD=4cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则
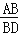 的值为( )
的值为( )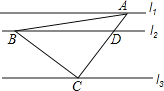
A.
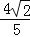 B.
B.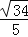 C.
C.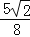 D.
D.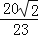
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,y1)和点Q(﹣2,y2)是一次函数y=﹣3x+m的图象上的两点,则y1,y2的大小关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )

A.19,20,14 B.19,20,20 C.18.4,20,20 D.18.4,25,20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是边长为5的正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.若EF=6,则CF的长为( )
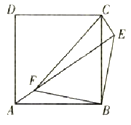
A. 6 B.
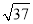 C.
C. 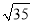 D.
D. 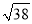
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识迁移:我们知道,一次函数y=a(x﹣m)+n(a≠0,m>0,n>0)的图象是由一次函数y=ax的图象向右平移m个单位,再向上平移n个单位得到;类似地,函数y=
 +n(k≠0,m>0,n>0)的图象是由反比例函数
+n(k≠0,m>0,n>0)的图象是由反比例函数 的图象向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
的图象向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).理解应用:(1)函数y=
 +1的图象可由函数y=
+1的图象可由函数y= 的图象向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
的图象向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .灵活应用:(2)如图,在平面直角坐标系xOy中,请根据所给的y=
 的图象画出函数y=
的图象画出函数y= ﹣2的图象,并根据该图象指出,当x在 时,y≥﹣1?
﹣2的图象,并根据该图象指出,当x在 时,y≥﹣1?
实际应用:
某老师对一位学生的学习情况进行跟踪研究,假设刚学完新知识时的记忆存留量为1,新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为y1=
 ;若在x=t(t≥4)时进行第一次复习,发现他复习后的记忆存留量是复习前的2倍(复习的时间忽略不计),且复习后的记忆存留量随x变化的函数关系为y2=
;若在x=t(t≥4)时进行第一次复习,发现他复习后的记忆存留量是复习前的2倍(复习的时间忽略不计),且复习后的记忆存留量随x变化的函数关系为y2= ,如果记忆存留量为
,如果记忆存留量为 时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
相关试题

