【题目】已知点A,B在数轴上分别表示m,n,其中m<n.
(1)填写下表;
m | 3 | ﹣6 | ﹣5 |
n | 5 | 4 | ﹣4 |
A,B两点的距离 |
|
|
|
(2)若A,B两点的距离为d,则d与m,n的数量关系为 ;
(3)若S=|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|,求S的最小值,并写出当S取最小值时x的取值范围.
参考答案:
【答案】(1)2,10,1;(2)d=|n﹣m|;(3)1088064.1010≤x≤1011
【解析】
(1)结合点在数轴上的位置进行计算;
(2)根据(1)即可发现规律:数轴上两点间的距离等于表示两个点的数的差的绝对值,或直接让较大的数减去较小的数;
(3)利用S=|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|是数轴上点x 与 3、4、5、…2018的距离和,进而得出当1010≤x≤1011 时,S最小求出即可.
(1)填写下表;
m | 3 | ﹣6 | ﹣5 |
n | 5 | 4 | ﹣4 |
A,B两点的距离 | 2 | 10 | 1 |
故答案为:2,10,1;
(2)d=n﹣m,
故答案为:d=n﹣m;
(3)根据绝对值的几何意义,|x﹣a|的意义是数轴上表示数x的点到表示数a的点之间的距离.
s=|x﹣3|
当x=3时,s有最小值s=0
s=|x﹣3|+|x﹣4|
当3≤x≤4 时,s有最小值s=4﹣3=1
s=|x﹣3|+|x﹣4|+|x﹣5|
当x=4时,S有最小值S=2
s=|x﹣3|+|x﹣4|+|x﹣5|+|x﹣6|
当4≤x≤5 时,S有最小值S=(6﹣3)+(5﹣4)=3+1=4
s=|x﹣3|+|x﹣4+|x﹣5|+|x﹣6|+|x﹣7|
当x=5时,S有最小值S=(7﹣3)+(6﹣4)+0=4+2=6,
…
根据观察所得规律
|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|共有(2018﹣3)+1=2016项
(2018+3)÷2=1010.5,
∴1010≤x≤1011,
当1010≤x≤1011时,S有最小值,
S=(2018﹣3)+(2017﹣4)+(2016﹣5)+…(1011﹣1010)
=2015+2013+2011+…+1
=![]() (2015+1)×1008
(2015+1)×1008
=1088064.
-
科目: 来源: 题型:
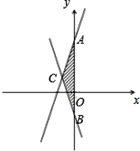
查看答案和解析>>【题目】已知,直线 y=2x+3 与直线 y= ﹣ 2x ﹣ 1.
( 1 )求两直线与 y 轴交点A,B的坐标;
( 2 )求两直线交点 C 的坐标;
( 3 )求 △ ABC 的面积.
-
科目: 来源: 题型:
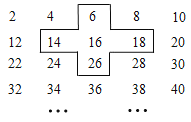
查看答案和解析>>【题目】探索规律:将连续的偶数2,4,6,8,…,排成如表:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)移动十字框,设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2560吗?若能,写出这五个数,若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排
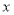 名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.(1)请写出此车间每天所获利润
 (元)与
(元)与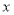 (人)之间的函数关系式;
(人)之间的函数关系式;(2)求自变量
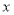 的取值范围;
的取值范围;(3)怎样安排生产每天获得的利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为
 ,
, ,
, ,
, , ……,则
, ……,则 的坐标为________________.
的坐标为________________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6 B. 6
 C. 3
C. 3 D. 3+3
D. 3+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)5(x+2)=2(5x-1)
(2)
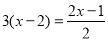
(3)
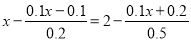
相关试题

