【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a﹣b+c>2.其中正确的结论的个数是( ) 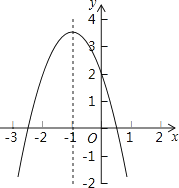
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣ ![]() =﹣1,
=﹣1,
∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以②正确;
∵b=2a,
∴2a﹣b=0,所以③错误;
∵x=﹣1时,y>0,
∴a﹣b+c>0,所以④正确.
故选C.
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
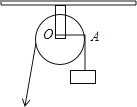
A.πcm
B.2πcm
C.3πcm
D.5πcm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写理由:
已知:如图,ABC是直线,∠1=115°,∠D=65°.
求证:AB∥DE.
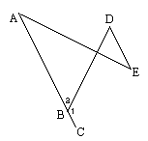
证明:∵ABC是一直线,(已知)
∴∠1+∠2=180°( )
∵∠1=115°(已知)
∴∠2=65°
又∵∠D=65°(已知)
∴∠2=∠D
∴ ∥ ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2
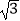 ,DE=2,则四边形OCED的面积( )
,DE=2,则四边形OCED的面积( ) 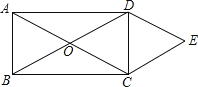
A.2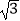
B.4
C.4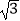
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
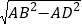 =8,CD=
=8,CD= =2,
=2,此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
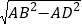 =8,CD=
=8,CD= =2,
=2,此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
-
科目: 来源: 题型:
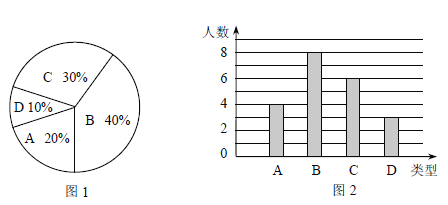
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:

① 小宇的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
相关试题

