搜索
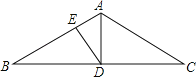
【题目】如图，在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于点E，若EA=2，则BE=（ ）
A．3 B．4 C．6 D．8
参考答案：
【答案】C
【解析】
试题分析：根据在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于点E，EA=2，可以求得AD⊥BC，∠B=∠C，以及∠B和∠C的度数，从而可以求得AD、AB的长，从而可以求得BE的长，本题得以解决．
解：∵在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，
∴AD⊥BC，∠B=∠C=30°，
∴∠ADC=90°，
∵DE⊥AB于点E，EA=2，
∴∠DEA=90°，∠DEB=90°，
∴∠BAD=60°，∠EDA=30°，
∴AD=2AE=4，
∴AB=2AD=8，
∴BE=AB﹣AE=8﹣2=6，
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用四舍五入法把3.1415926精确到千分位是_______；近似数3.0×106精确到______位.
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：
（1）3（x+1）=9；
（2）
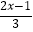=1﹣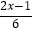 
． -
科目： 来源： 题型：
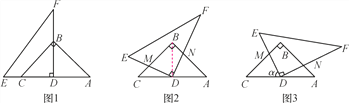
查看答案和解析>>【题目】(12分)如图1，已知Rt△ABC中，AB＝BC，AC＝2，把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE，长直角边为DF)，点C在DE上，点B在DF上．
(1)求重叠部分△BCD的面积；
(2)如图2，将直角三角板DEF绕D点按顺时针方向旋转30度，DE交BC于点M，DF交AB于点N.
①求证：DM＝DN；
②在此条件下重叠部分的面积会发生变化吗？若发生变化，请求出重叠部分的面积，若不发生变化，请说明理由；
(3)如图3，将直角三角板DEF绕D点按顺时针方向旋转α度(0＜α＜90)，DE交BC于点M，DF交AB于点N，则DM＝DN的结论仍成立吗？重叠部分的面积会变吗？(请直接写出结论，不需要说明理由)
-
科目： 来源： 题型：
查看答案和解析>>【题目】中考英语听力测试期间T需要杜绝考点周围的噪音．如图，点A是某市一中考考点，在位于考点南偏西15°方向距离500米的C点处有一消防队．在听力考试期间，消防队突然接到报警电话，消防车需沿北偏东75°方向的公路CF前往救援．已知消防车的警报声传播半径为400米，若消防车的警报声对听力测试造成影响，则消防车必须改道行驶．试问：消防车是否需要改道行驶？
说明理由．（
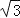≈1.732）
-
科目： 来源： 题型：
查看答案和解析>>【题目】 如图，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4．则下列结论错误的是（ ）.
A．AE∥BC B． ∠ADE=∠BDC
C．△BDE是等边三角形 D． △ADE的周长是9
-
科目： 来源： 题型：
查看答案和解析>>【题目】若△ABC∽△DEF ， 若∠A=50°，∠B=60°，则∠F的度数是（ ）
A.50°
B.60°
C.70°
D.80°
相关试题
