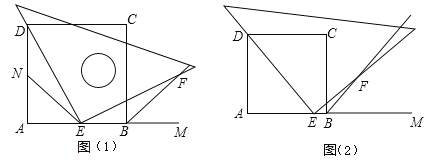
【题目】如图所示,四边形![]() 是正方形,
是正方形, ![]() 是
是![]() 延长线上一点.直角三角尺的一条直角边经过点
延长线上一点.直角三角尺的一条直角边经过点![]() ,且直角顶点
,且直角顶点![]() 在
在![]() 边上滑动(点
边上滑动(点![]() 不与点
不与点![]() 重合),另一直角边与
重合),另一直角边与![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .
.
(1)求证: ![]() ;
;
(2)如图(1),当点![]() 在
在![]() 边的中点位置时,猜想
边的中点位置时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
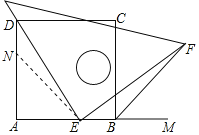
(3)如图(2),当点![]() 在
在![]() 边(除两端点)上的任意位置时,猜想此时
边(除两端点)上的任意位置时,猜想此时![]() 与
与![]() 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想.
参考答案:
【答案】(1)详见解析;(2)![]() ,理由详见解析;(3)
,理由详见解析;(3)![]() ,理由详见解析
,理由详见解析
【解析】
(1)根据![]() ,等量代换即可证明;(2)DE=EF,连接NE,在DA边上截取DN=EB,证出△DNE≌△EBF即可得出答案;(3)在
,等量代换即可证明;(2)DE=EF,连接NE,在DA边上截取DN=EB,证出△DNE≌△EBF即可得出答案;(3)在![]() 边上截取
边上截取![]() ,连接
,连接![]() ,证出
,证出![]() 即可得出答案.
即可得出答案.
(1)证明:∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2) ![]() 理由如下:
理由如下:
如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∵![]() 分别为
分别为![]() 中点
中点
∴![]() ,
,
∴![]()
又∵![]()
∴![]()
∴![]() ,
,
又∵![]() ,
,![]() 平分
平分![]()
∴![]() .
.
∴![]()
在![]() 和
和![]() 中
中
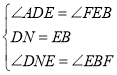
![]() ,
,
∴![]()
(3) ![]() .理由如下:
.理由如下:
如图,在![]() 边上截取
边上截取![]() ,连接
,连接![]() ,
,

∵四边形![]() 是正方形,
是正方形, ![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]()
∴![]() ,
,
∵![]() 平分
平分![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
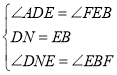
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校要用长24米的篱笆围成一个长方形生物园ABCD,EF是ABCD内用篱笆做成的竖直隔断.为了节约材料,场地的一边CD借助原有的一面墙,墙长为12米,长方形生物园ABCD的面积为45平方米,求长方形场地的边AD的长.
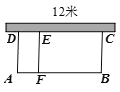
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学兴趣小组活动中,小明利用同弧所对的圆周角及圆心角的性质探索了一些问题,下面请你和小明一起进入探索之旅.
(1)如图1,△ABC中,∠A=30°,BC=2,则△ABC的外接圆的半径为 ;
(2)如图2,在矩形ABCD中,请利用以上操作所获得的经验,在矩形ABCD内部用直尺与圆规作出一点P,点P满足;∠BPC=∠BEC,且PB=PC;(要求:用直尺与圆规作出点P,保留作图痕迹.)
(3)如图3,在平面直角坐标系的第一象限内有一点B,坐标为(2,m),过点B作AB⊥y轴,BC⊥x轴,垂足分别为A、C,若点P在线段AB上滑动(点P可以与点A、B重合),发现使得∠OPC=45°的位置有两个,则m的取值范围为 .
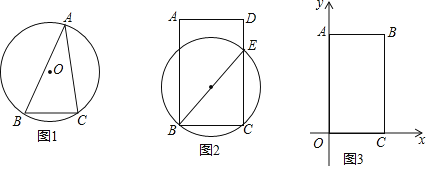
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出无鱼水缸内最高水位
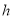 与注水时间
与注水时间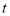 之间的变化情况的是( )
之间的变化情况的是( )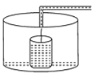
A.
 B.
B.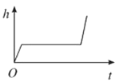
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
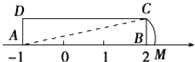
【答案】
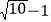
【解析】AC=AM=
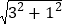 =
= ,∴AM=
,∴AM=
【题型】填空题
【结束】
11【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
相关试题

