【题目】已知线段AB,延长AB到C,使BC=![]() AB,D为AC的中点,若BD=6.
AB,D为AC的中点,若BD=6.
(1)画出图形,求AB的长;
(2)若点E在直线AB上,AE=3,求线段ED的长;
(3)若点F在直线AB上,AF=k,求线段FD的长(请直接写出答案、用含k的式子表示).
参考答案:
【答案】(1)16,图形见解析(2)7或13 (3)10+k或10﹣k或k﹣10
【解析】
(1)设BC=x,则AB=4x,依据D为AC中点,可得AD=CD=2.5x,依据BD=6,可得方程2.5x﹣x=6,解得x=4,即可得到AB=16;
(2)如图2,需要分两种情况讨论,(ⅰ)当点E在点A的右边时,(ⅱ)当点E在点A的左边时,根据线段的和差即可得到结论;
(3)如图3,需要分三种情况讨论,(a)当点F在点A的左边时,(b)当点F在点A的右边且在点D的左边时,(c)当点F在点D的右边时,根据线段的和差即可得到结论.
解:(1)如图1,设BC=x,则AB=4x,
∵D为AC中点,
∴AD=CD=2.5x,
∵BD=CD﹣BC=6,
∴2.5x﹣x=6,
解得x=4,
∴AB=16;
(2)如图2,
(ⅰ)当点E在点A的右边时,
由(1)知,AD=2.5x=10,
∵AE=3,
∴DE=AD﹣AE=10-3=7;
(ⅱ)当点E在点A的左边时,
DE=AD+AE=10+3=13;
综上所述,线段ED的长为:7或13;
(3)如图3,
(a)当点F在点A的左边时,DF1=AD+AF1=10+k,
(b)当点F在点A的右边且在D的左边时,DF2=AD﹣AF2=10﹣k,
(c)当点F在点D的右边时,DF3=AF3﹣AD=k﹣10,
综上所述,线段FD的长为:10+k或10﹣k或k﹣10
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.
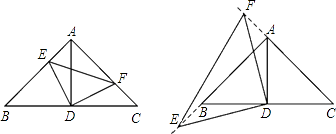
(1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD;
(2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到点A、B时停止;设△DEF的面积为y,F点运动的时间为x,求y与x的函数关系式;
(3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续运动,求此时y与x的函数关系式. -
科目: 来源: 题型:
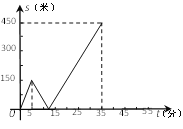
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距
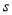 (米),甲行走的时间为
(米),甲行走的时间为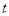 (分),
(分),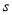 关于
关于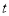 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.(1)求甲行走的速度;
(2)在坐标系中,补画
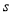 关于
关于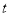 函数图象的其余部分;
函数图象的其余部分;(3)问甲、乙两人何时相距360米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( )
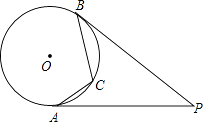
A.80°
B.110°
C.120°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
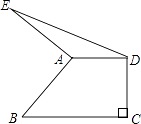
A.10
B.11
C.12
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
…… -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABMD=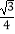 AM2 .
AM2 .
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
相关试题

