【题目】二次函数y=(x﹣1)2+k分别与x轴、y轴交于A、B、C三点,点A在点B的左侧,直线y=﹣ ![]() x+2经过点B,且与y轴交于点D.
x+2经过点B,且与y轴交于点D.
(1)如图1,求k的值;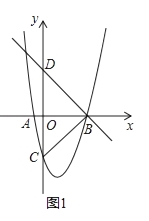
(2)如图2,在第一象限的抛物线上有一动点P,连接AP,过P作PE⊥x轴于点E,过E作EF⊥AP于点F,过点D作平行于x轴的直线分别与直线FE、PE交于点G、H,设点P的横坐标为t,线段GH的长为d,求d与t的函数关系式,并直接写出t的取值范围;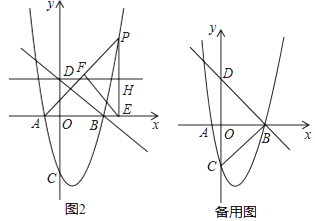
(3)在(2)的条件下,过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N,tan∠MEA= ![]() ,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
参考答案:
【答案】
(1)解:在一次函数y=﹣ ![]() x+2中,令y=0,得:0=﹣
x+2中,令y=0,得:0=﹣ ![]() x+2,
x+2,
解得x=3,
∴B(3,0).
令x=0得y=2,
∴D(0,2).
将B(3,0),代入y=(x﹣1)2+k得:4+k=0,
∴k=﹣4.
(2)解:如答图1所示:
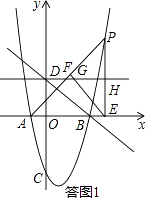
∵PE⊥x轴,EF⊥AP,
∴∠PEA=∠EFA=90°
∵∠PEF+∠FEA=90°,∠PAE+∠FEA=90°
∴∠PEF=∠PAE.
∵DH∥x轴 HE⊥x轴
∴∠HDO=∠DOE=∠PEO=90°
∴四边形DOEH为矩形.
∴HE=2.
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴d=2t﹣6.(t>3).
(3)解:∵∠TGH=∠GTE=∠TEH=90°,
∴GHET为矩形.
∴GH=d=ET=2t﹣6.
∵tan∠MEB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴MT=3t﹣9.
∵ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ,
,
解得t=4.
∴P(4,5).
∴AT=AE﹣ET=t+1﹣(2t﹣6)=7﹣t=3.
∴M(2,3)
把x=2代入y=x2﹣2x﹣3中,得N(2,﹣3)
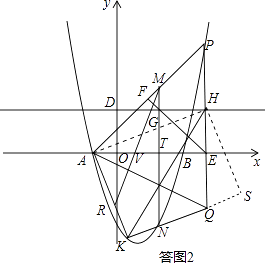
∴MT=TN=AT,∠MAT=90°.
∵∠RAE﹣∠RMA=45°,
∴∠RAE﹣45°=∠RMA,
∴∠RAM=∠RMA,
∵S△AKQ=S△HKQ,作HW⊥KQ.
∴AK∥HW,AK=HW,
∴四边形AKWH是矩形,
∴∠RAH=∠HAK=90°,
∴∠RAM=∠HAN.
∵A(﹣1,0),H(4,2),N(2,﹣3),
∴AH=HN= ![]() ,
,
∴∠HAN=∠HNA=∠RAM=∠RMA.
又∵AM=AN,
∴△RAM≌△HAN,
∴AR=AH.
过R作RL⊥x轴,
∴∠RLA=∠AEH=90°,
∵∠RAL+∠HAE=90,∠HAE+∠AHE=90,
∴∠RAL=∠AHE,
∴△ARL≌△AHE.
∴RL=AE=5,AL=HE=3
∴R(﹣3,5).
由∠RAM﹣∠RMA=45°可知∠RAV=∠RVA,∠RMT=∠HAE,tan∠RMT=tan∠HAE= ![]() ,V(
,V( ![]() ,0),
,0),
直线MR的解析式为y= ![]() x﹣2,直线AK的解析式为y=﹣
x﹣2,直线AK的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
交点R(﹣ ![]() ,
, ![]() ).
).
【解析】(1)先求出一次函数与两坐标轴的交点B、D的坐标,再将点B的坐标代入二次函数解析式即可求得k的值。
(2)根据已知PE⊥x轴,EF⊥AP,得出∠PEA=∠EFA=90°,再根据同角的余角相等,证得∠PEF=∠PAE.根据矩形的性质得出HE=2.然后利用三角形函数的定义得出线段成比例,建立方程,可求出d与t的函数关系式及x的取值范围。
(3)利用(2)中求得的函数关系式,根据矩形的性质及三角函数的定义先求出点P和点M的坐标,由MN平行y轴,因此将x=2代入二次函数解析式,即可求得点N的坐标,即可得出MT=TN=AT,添加辅助线作HS⊥KQ.去证明四边形AKSH是矩形,推出∠RAM=∠HAN,再证明△RAM≌△HAN,得出AR=AH.过R作RL⊥x轴,易正明△ARL≌△AHE.得出RL=AE=5,AL=HE=3,可得到点R的坐标,再求出直线MR的解析式和直线AK的解析式,即可求出两直线的交点R的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.

(1)写出图中所有相等的角和相等的线段;
(2)当BF=8cm,AD=7 cm时,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;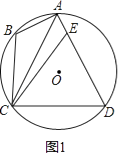
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;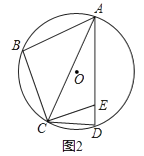
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC=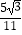 ,EG=2,求AE的长.
,EG=2,求AE的长.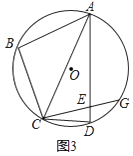
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用一根长是20 cm的细绳围成一个长方形,这个长方形的一边长为x cm,它的面积为y cm2.

(1)写出y与x之间的关系式;
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面的表格中,你看出什么规律?(写出一条即可)
(4)从表格中可以发现怎样围,得到的长方形的面积最大?最大是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC=CA,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t(s)后,它们分别爬行到了D,E处,设DC与BE的交点为F.
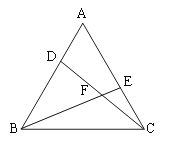
(1)△ACD≌△CBE吗?为什么?
(2)小蚂蚁在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
相关试题

