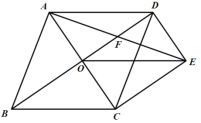
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
参考答案:
【答案】(1)证明见解析;(2)AE=![]() .
.
【解析】
(1)先证得OCED是平行四边形,再根据菱形的对角线互相垂直得到∠COD=90°,证得OCED是矩形,即可证明OE=CD;
(2)由菱形的性质和勾股定理求出AC与CE的长,最后根据勾股定理解答即可..
解:(1)∵在菱形ABCD中,
∴OC=![]() AC,AC⊥BD.
AC,AC⊥BD.
又∵DE:AC=1:2
∴DE=![]() AC
AC
∴DE=OC
∵DE//AC,
∴四边形OCED是平行四边形.
∵∠COD=90°
∴平行四边形OCED是矩形.
∴OE=CD
(2)∵在姜形ABCD中,
∴AB=BC=CD=AD=2,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,AO=1.
∵在矩形OCED中,CE=OD=![]()
又∵矩形DOCE中,∠OCE=90°
∴在Rt△ACE中,AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(或方程组)解应用题2019年是决胜全面建成小康社会、打好污染防治攻坚战的关键之年.为了解决垃圾回收最后一公里的难题,“小黄狗”智能垃圾分类回收环保公益项目通过大数据、人工智能和物联网等先进科技进驻小区、写字楼、学校、机关和社区等进行回收.某位小区居民装修房屋,在过去的一个月内投放纸类垃圾和塑料垃圾共82公斤,其中纸类垃圾的投放是塑料垃圾的8倍多10公斤,请问这位小区居民在过去的一个月内投放纸类垃圾和塑料垃圾分别是多少公斤?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:对于(x﹣1)(x﹣3)>0,这类不等式,我们可以进行下面的解题思路由有理数的乘法法则“两数相乘,同号得正”,可得(1)
 或(2)
或(2) 从而将未知的一元二次不等式转化为学过的一元一次不等式组,分别解这两个不等式组,即可求得原不等式的解集,即:解不等式组(1)得x>3,解不等式组(2)得x<1,所以(x﹣1)(x﹣3)>0的解集为x>3或x<1.
从而将未知的一元二次不等式转化为学过的一元一次不等式组,分别解这两个不等式组,即可求得原不等式的解集,即:解不等式组(1)得x>3,解不等式组(2)得x<1,所以(x﹣1)(x﹣3)>0的解集为x>3或x<1.请根据以上材料回答下面问题:
(1)直接写出(x﹣2)(x﹣5)<0的解集;
(2)仿照上述材料,求
 >0的解集.
>0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
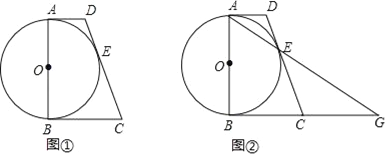
(1)求证:BC为⊙O的切线;
(2)连接AE并延长与BC的延长线交于点G(如图②所示).若AB=
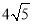 ,CD=9,求线段BC和EG的长.
,CD=9,求线段BC和EG的长.
相关试题

