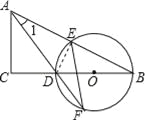
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=2
,EF=2![]() ,求CD的长.
,求CD的长.

参考答案:
【答案】(1)证明见解析(2)3
【解析】试题分析:(1)连接DE,由BD是⊙O的直径,得到∠DEB=90°,由于E是AB的中点,得到DA=DB,根据等腰三角形的性质得到∠1=∠B等量代换即可得到结论;(2)根据等腰三角形的判定定理得到AE=EF=2![]() ,推出AB=2AE=4
,推出AB=2AE=4![]() ,在Rt△ABC中,根据勾股定理得到BC=
,在Rt△ABC中,根据勾股定理得到BC=![]() =8,设CD=x,则AD=BD=8﹣x,根据勾股定理列方程即可得到结论.
=8,设CD=x,则AD=BD=8﹣x,根据勾股定理列方程即可得到结论.
试题解析:(1)连接DE, ∵BD是⊙O的直径, ∴∠DEB=90°, ∵E是AB的中点, ∴DA=DB,
∴∠1=∠B, ∵∠B=∠F, ∴∠1=∠F;
(2)∵∠1=∠F, ∴AE=EF=2![]() , ∴AB=2AE=4
, ∴AB=2AE=4![]() ,
,
在Rt△ABC中,AC=ABsinB=4, ∴BC=![]() =8,
=8,
设CD=x,则AD=BD=8﹣x, ∵AC2+CD2=AD2, 即42+x2=(8﹣x)2, ∴x=3,即CD=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料,再解决问题: 阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去一层根号.
例如: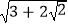 =
= 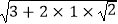 =
= 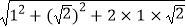 =
=  =|1+
=|1+ 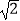 |=1+
|=1+ 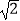
(1)解决问题: 模仿上例的过程填空: =
= 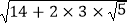 ====
====
(2)根据上述思路,试将下列各式化简. ①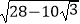 ②
②  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
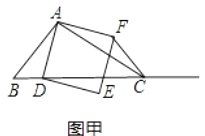
(1)如果AB=AC,∠BAC=90°, ①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 , 数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?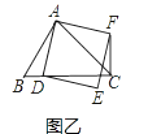
(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动
 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).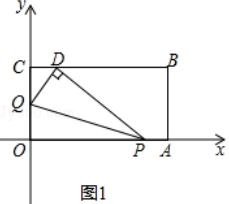
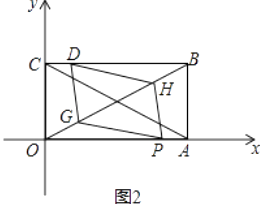
(1)求点B的坐标,并用含t的代数式表示OP,OQ;
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证:当t=1时四边形DGPH是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,P是四边形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1 , S2 , S3 , S4 , 则一定成立的是( )

A.S1+S2>S3+S4
B.S1+S2=S3+S4
C.S1+S2<S3+S4
D.S1+S3=S2+S4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(1,﹣2),则点P关于x轴的对称点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a﹣2|+b2﹣2b+1=0,则a=__,b=__.
相关试题

