【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.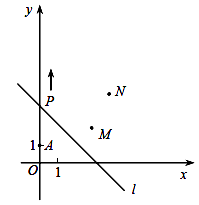
(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
参考答案:
【答案】
(1)解:直线y=-x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,b=1+t.
当t=3时,b=4,
故y=-x+4.
(2)解:当直线y=-x+b过点M(3,2)时,
2=-3+b,
解得:b=5,
5=1+t,
解得t=4.
当直线y=-x+b过点N(4,4)时,
4=-4+b,
解得:b=8,
8=1+t,
解得t=7.
故若点M,N位于l的异侧,t的取值范围是:4<t<7.
(3)解:如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
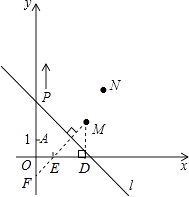
过点M作MD⊥x轴于点D,则OD=3,MD=2.
已知∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,-1).
∵M(3,2),F(0,-1),
∴线段MF中点坐标为( ![]() ,
, ![]() ).
).
直线y=-x+b过点( ![]() ,
, ![]() ),则
),则 ![]() =-
=- ![]() +b,解得:b=2,
+b,解得:b=2,
2=1+t,
解得t=1.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=-x+b过点(2,1),则1=-2+b,解得:b=3,
3=1+t,
解得t=2.
故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上.
【解析】(1)利用直线的平移规律,上加下减,可求出解析式;(2)l令直线y=-x+b过点M、N,求出这两个临界点对应的t值,t的范围就是介于这两个值之间;(3)坐标轴包括x、y轴,分两类,利用轴对称的性质,求出t值.
-
科目: 来源: 题型:
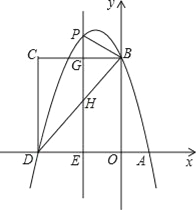
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(﹣3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形的长比宽大5,其周长为50,求其长、宽各是多少.设宽为x,列方程为_____.
-
科目: 来源: 题型:
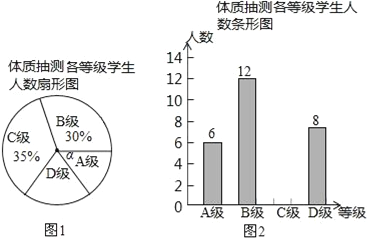
查看答案和解析>>【题目】为了进一步了解义务教育阶段学生的体质健康状况,某县从全县九年级学生中随机抽取了部分学生进行了体质抽测.体质抽测的结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格.并根据抽测结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)本次抽测的学生人数是 人;
(2)图(1)中∠α的度数是 ,并把图(2)条形统计图补充完整;
(3)该县九年级有学生4800名,如果全部参加这次体质测试,请估计不合格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中H为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2(x-2)-3(x+1)=-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积.
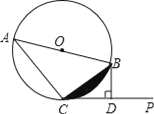
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象是数学中的平移的是( )
A. 小朋友荡秋千
B. 碟片在光驱中运行
C. “神舟”十号宇宙飞船绕地球运动
D. 瓶装饮料在传送带上移动
相关试题

