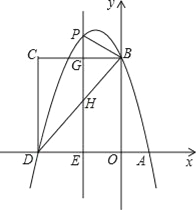
【题目】如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(﹣3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+4;(2)PG=﹣
x+4;(2)PG=﹣![]() m2﹣
m2﹣![]() m+4﹣4=﹣
m+4﹣4=﹣![]() m2﹣
m2﹣![]() m(﹣2<m<0);(3)在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或﹣
m(﹣2<m<0);(3)在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或﹣![]() .
.
【解析】试题分析:(1)设交点式y=a(x﹣1)(x+3),然后把B点坐标代入求出a即可得到抛物线解析式;
(2)先解方程﹣![]() x2﹣
x2﹣![]() x+4=4,解得x1=0,x2=﹣2,则﹣2<m<0,设P(m,﹣
x+4=4,解得x1=0,x2=﹣2,则﹣2<m<0,设P(m,﹣![]() m2﹣
m2﹣![]() m+4),G(m,4),则可用m表示PG;
m+4),G(m,4),则可用m表示PG;
(3)易得△DEH∽△DOB,则判定△PGB与△BOD,由于∠PGB=∠DOB,根据相似三角形的判定方法,当![]() 时,△PGB∽△BOD,则△PGB∽△HED,当
时,△PGB∽△BOD,则△PGB∽△HED,当![]() 时,△PGB∽△DOB,则△PGB∽△DEH,然后分别利用相似比列关于m的方程,再解方程求出m,从而得到满足条件的m的值.
时,△PGB∽△DOB,则△PGB∽△DEH,然后分别利用相似比列关于m的方程,再解方程求出m,从而得到满足条件的m的值.
试题解析:(1)设抛物线解析式为y=a(x﹣1)(x+3),
把B(0,4)代入得a(﹣1)3=4,解得a=﹣![]() ,
,
所以抛物线解析式为y=﹣![]() (x﹣1)(x+3),
(x﹣1)(x+3),
即y=﹣![]() x2﹣
x2﹣![]() x+4;
x+4;
(2)当y=4时,﹣![]() x2﹣
x2﹣![]() x+4=4,解得x1=0,x2=﹣2,
x+4=4,解得x1=0,x2=﹣2,
∴﹣2<m<0,
∵E(m,0),PE⊥x轴,
∴P(m,﹣![]() m2﹣
m2﹣![]() m+4),
m+4),
而BC∥x轴,
∴G(m,4),
∴PG=﹣![]() m2﹣
m2﹣![]() m+4﹣4=﹣
m+4﹣4=﹣![]() m2﹣
m2﹣![]() m(﹣2<m<0);
m(﹣2<m<0);
(3)∵HE∥OB,
∴△DEH∽△DOB,
∵∠PGB=∠DOB,
∴当![]() 时,△PGB∽△BOD,则△PGB∽△HED,
时,△PGB∽△BOD,则△PGB∽△HED,
即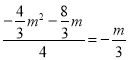 ,整理得m2+m=0,解得m1=0(舍去),m2=﹣1,
,整理得m2+m=0,解得m1=0(舍去),m2=﹣1,
当![]() 时,△PGB∽△DOB,则△PGB∽△DEH,
时,△PGB∽△DOB,则△PGB∽△DEH,
即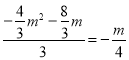 ,整理得16m2+23m=0,解得m1=0(舍去),m2=﹣
,整理得16m2+23m=0,解得m1=0(舍去),m2=﹣![]() ,
,
综上所述,在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:3(a2+2b)-(2a2-b),其中a=-2,b=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )
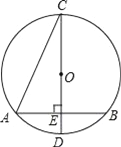
A. 4cm B. 3
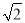 cm C. 2
cm C. 2 cm D. 2
cm D. 2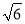 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为
 ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形的长比宽大5,其周长为50,求其长、宽各是多少.设宽为x,列方程为_____.
-
科目: 来源: 题型:
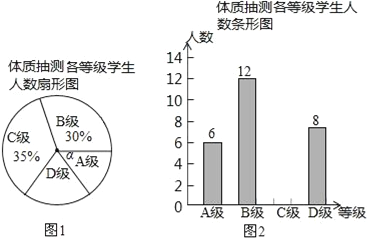
查看答案和解析>>【题目】为了进一步了解义务教育阶段学生的体质健康状况,某县从全县九年级学生中随机抽取了部分学生进行了体质抽测.体质抽测的结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格.并根据抽测结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)本次抽测的学生人数是 人;
(2)图(1)中∠α的度数是 ,并把图(2)条形统计图补充完整;
(3)该县九年级有学生4800名,如果全部参加这次体质测试,请估计不合格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中H为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
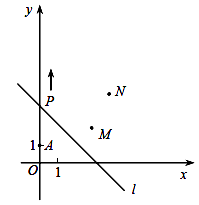
(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
相关试题

