Question

【题目】如图1，在平面直角坐标系中，点，，点在第三象限，已知，且．

（1）求点的坐标；

图1

（2）如图2，为线段上一动点（端点除外），是轴负半轴的一点，连接、，射线与的角平分线交于，若，求点的坐标；

图2

（3）在第（2）问的基础上，如图3，点与点关于轴对称，是射线上一个动点，连接，平分，平分，射线．试问的度数是否发生改变？若不变，请求其度数：若改变，请指出其变化范围．

图3

Answer 1

【答案】（1）；（2）；（3）的度数不变，且．

【解析】

(1)根据垂直和平行求出点C的坐标；

(2)作于点，作，根据即可得到答案；

(3)作，平分，平分，计算即可得到答案；

（1）解：，，

，

∵AC⊥AB，

，

（2）解：作于点，作，如图，

，，，

，

，

，，

，

，

，

平分，

，

，

；

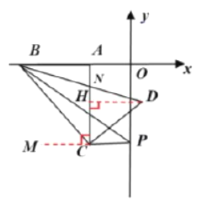
（3）答：的度数不变，且，

由第（2）问得轴，

，

作轴，

，，

①

平分，平分，

设，，

①式即为，

，

，

，

.