【题目】如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.则ABCD的周长为_____,面积为_____.

参考答案:
【答案】39cm60cm2
【解析】
根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13cm,根据等腰三角形的性质得到AB=CD=![]() AD=
AD=![]() CD=6.5cm,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
CD=6.5cm,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
∵BE、CE分别平分∠ABC、∠BCD,
∴∠1=∠3=![]() ∠ABC,∠DCE=∠BCE=
∠ABC,∠DCE=∠BCE=![]() ∠BCD,
∠BCD,
∵AD∥BC,AB∥CD,
∴∠2=∠3,∠BCE=∠CED,∠ABC+∠BCD=180°,
∴∠1=∠2,∠DCE=∠CED,∠3+∠BCE=90°,
∴AB=AE,CD=DE,∠BEC=90°,
在Rt△BCE中,根据勾股定理得:BC=13cm,
根据平行四边形的对边相等,得到:AB=CD,AD=BC,
∴平行四边形的周长等于:AB+BC+CD+AD=6.5+13+6.5+13=39cm;
作EF⊥BC与F,根据直角三角形的面积公式得:EF=![]() cm,
cm,
∴S平行四边形ABCD=BC·EF=![]() =60cm2,
=60cm2,
故答案为:39cm,60cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l和双曲线
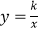 (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )
(k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( ) 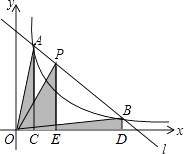
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
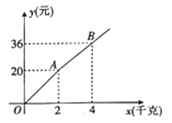
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:


(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB的解析式为y=
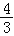 x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.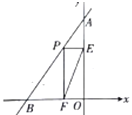
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝即将到来的2018年国庆节,某校举行了书法比赛,赛后整理了参赛同学的成绩,并制作了如下两幅不完整的统计图表
分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x<100
20
0.1
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= .
(2)请补全频数直方图;
(3)若绘制扇形统计图,则分数段60≤x<70所对应的扇形的圆心角的度数是 .

相关试题

