【题目】如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是 . 
参考答案:
【答案】5+ ![]()
【解析】解:连接CD; ∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE与△CFD中,  ,
,
∴△ADE≌△CDF(SAS);
∴ED=DF,∠CDF=∠EDA;
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形,
∵∠C=90°,AC=BC=5,
∴AB=5 ![]() ,
,
∴当,△CEF周长的最小时,EF取最小值,
∴E、F分别为AC、BC中点时,EF的值最小,
∴EF= ![]() AB=
AB= ![]() ,
,
∴△CEF周长的最小值=CE+CF+EF=AE+CE+EF=AC+EF=5+ ![]() ;
;
所以答案是:5+ ![]() .
.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2+2mx+64是完全平方式,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a(n-1)2-2a(n-1)+a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
①l1和l2的距离为2 ②MN=
 ③当直线MN与⊙O相切时,∠MON=90°
③当直线MN与⊙O相切时,∠MON=90°④当AM+BN=
 时,直线MN与⊙O相切.正确的个数是( )
时,直线MN与⊙O相切.正确的个数是( )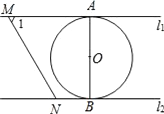
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】无论m取什么实数,点A(m+1,2m﹣2)都在直线l上.若点B(a,b)是直线l上的动点,则(2a﹣b﹣6)3的值等于____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形三边长分别为l、3、x,且x为整数,则此三角形的周长是( )
A. 9 B. 8 C. 7 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别在∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,点D在点F的右侧,O为圆心.
(1)求证:△ABD≌△AFE
(2)若AB=4
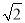 ,8
,8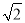 <BE≤4
<BE≤4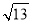 ,求⊙O的面积S的取值范围.
,求⊙O的面积S的取值范围.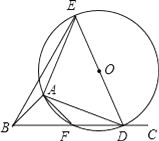
相关试题

