【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下 :
:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)计算上述试验中“4朝下”的频率是多少?
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是 ![]() .”的说法正确吗?为什么?
.”的说法正确吗?为什么?
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
参考答案:
【答案】
(1)
“4朝下”的频率: ![]() ;…
;…
故答案为: ![]() .
.
(2)
这种说法是错误的.在60次试验中,“2朝下”的频率为 ![]() .
.
并不能说明“2朝下”这一事件发生的概率为 ![]() .只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
.只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
(3)
随机投掷正四面体两次,所有可能出现的结果如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
总共有16种结果,每种结果出现的可能性相同,而两次朝下数字之和大于4的结果有10种.
∴P(朝下数字之和大于4)= ![]()
【解析】本题主要考查列表法与树状图法求概率,以及频率的意义,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.(1)先由频率=频数÷试验次数算出频率;(2)根据表格观察抛掷的次数增多时,频率稳定到哪个数值,这就是概率.(3)列表列举出所有的可能的结果,然后利用概率公式解答即可.
【考点精析】掌握用频率估计概率是解答本题的根本,需要知道在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一个均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数1向上代表肉馅,点数2向上代表香肠馅,点数3,4向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.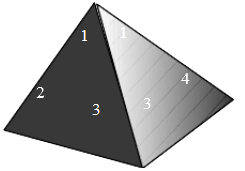
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
-
科目: 来源: 题型:
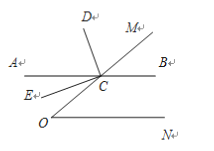
查看答案和解析>>【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
-
科目: 来源: 题型:
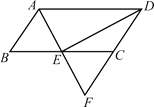
查看答案和解析>>【题目】在□
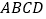 中,
中,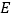 是
是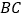 的中点,连接
的中点,连接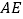 并延长交
并延长交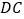 的延长线于点
的延长线于点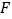 .
.(1)求证:
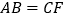 ;
;(2)连接
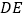 ,若
,若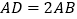 ,求证:
,求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:对非负数x“四舍五入”到个位的值记为<x>,
即当n为非负数时,若
 ,则<x>=n.
,则<x>=n.例如<0>=<0.49>=0,<0.5>=<1.49>=1,<2>=2,<3.5>=<4.23>=4,…
试回答下列问题:
(1)填空: <9.6>=_________;
如果<x>=2,实数x的取值范围是________________.
(2)若关于x的不等式组
 的整数解恰有4个,求<m>的值;
的整数解恰有4个,求<m>的值;(3)求满足
 的所有非负实数x的值.
的所有非负实数x的值.
相关试题

